
|
Noções de Probabilidade e Estatística
|
Parte 3 - Probabilidades
1 Probabilidades
A teoria das probabilidades é o ramo da matemática que desenvolve e avalia modelos para descrever fenômenos aleatórios. É a base teórica para o desenvolvimento das técnicas estatísticas.
Consiste em descrever o conjunto de resultados possíveis do fenômeno e atribuir pesos a cada possível resultado, refletindo suas chances de ocorrência, estes pesos são as chamadas probabilidades.
2 Fenômenos determinísticos e aleatórios
Os fenômenos podem ser classificados como determinísticos e aleatórios dependendo de como ocorre seu desfecho em diversas tentativas.
Fenômenos determinísticos: algo que, quando repetido diversas vezes, tem sempre o mesmo desfecho, isto é, o mesmo resultado.
Fenômenos aleatórios: algo que, quando repetido diversas vezes, pode ter diferentes desfechos. É tratado como aleatório pois antes da execução não há como saber qual dos possíveis resultados será observado. Portanto, um fenômeno aleatório é uma situação ou acontecimento cujos resultados não podem ser previstos com certeza.
3 Teoria dos Conjuntos
Eventos são resultados ou um subconjunto de resultados de um experimento aleatório, usualmente são representados por letras latinas maiúsculas (A, B, C, …). A teoria dos conjuntos é utilizada para definir operações com eventos. Alguns conceitos importantes são:
- Espaço amostral: conjunto de todos os resultados possíveis de um fenômeno aleatório. Denotado por \(\Omega\). Os subconjuntos de \(\Omega\) são os eventos. O espaço amostral pode ser:
- Discreto: contêm apenas um número finito ou contável de elementos.
- Contínuo: contêm um número infinito de elementos.
\(\\\)
Conjunto vazio: conjunto sem elementos, denotado por \(\phi\).
União: sejam dois eventos \(A\) e \(B\), a união é denotada por \(A ∪ B\) e representa a ocorrência de, pelo menos, um dos eventos A ou B.
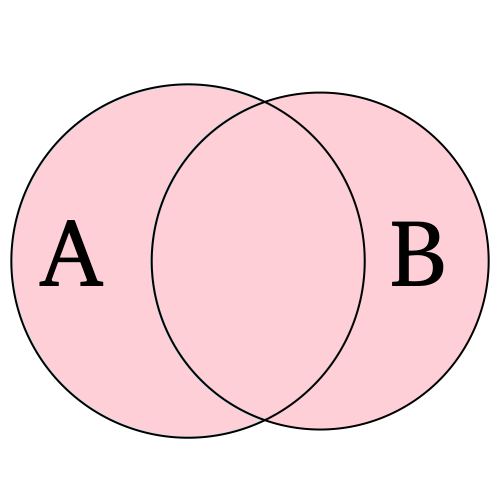
- Interseção: sejam dois eventos \(A\) e \(B\), a interseção é denotada por \(A ∩ B\) e representa a ocorrência simultânea de A e B.
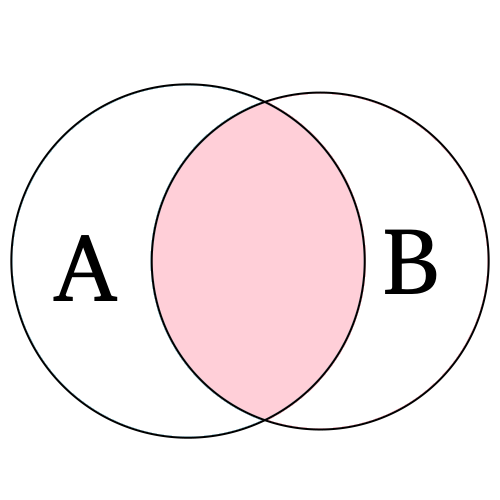
- Eventos disjuntos ou mutualmente exclusivos: sejam dois eventos \(A\) e \(B\), eles são ditos disjuntos se possuem interseção nula, isto é, não têm elementos em comum. \(A ∩ B = \phi\).
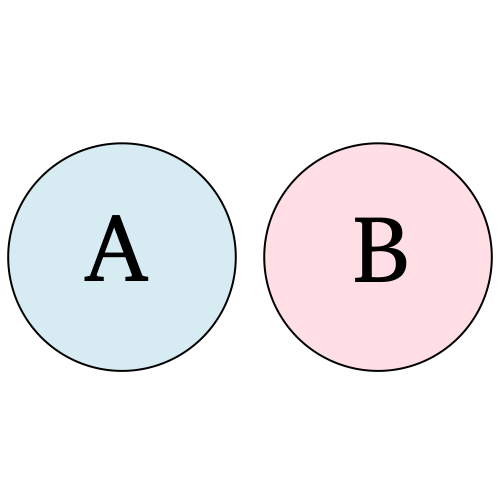
- Eventos complementares: eventos que a união resulta no espaço amostral e a intersecção é vazia. \(A ∪ A^{c} = \Omega\) e \(A ∩ A^{c} = \phi\).
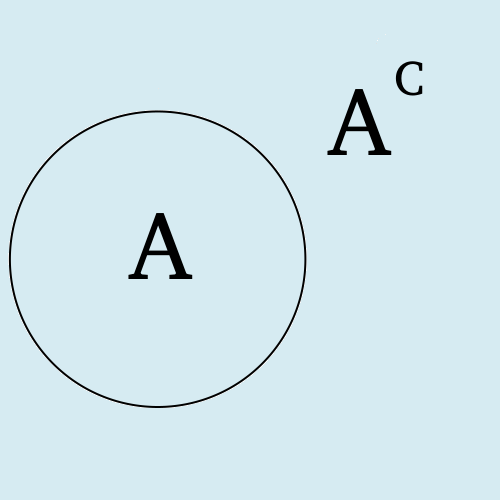
4 Definição axiomática de probabilidade
Probabilidade é uma função \(P(·)\) que atribui valores que mensuram a chance de ocorrência de eventos do espaço amostral, de tal forma que que atenda as condições:
\(0 \leq P(A) \leq 1, \forall A \in \Omega\)
\(P(\Omega) = 1\)
\(P \left ( ∪_{j=1}^{n} A_{j} \right ) = \sum_{j=1}^{n} P(A_{j})\), desde que os \(A_{j}\) sejam disjuntos.
Considerando o que foi apresentado até o momento, o problema agora é: como atribuir probabilidades aos elementos do espaço amostral?
As principais maneiras de atribuir probabilidades são:
A forma clássica: baseia-se nas características teóricas da realização do fenômeno.
A forma frequentista: baseia-se nas frequências de ocorrência do fenômeno. Para um grande número de repetições, a frequência relativa dos eventos do espaço amostral são estimativas da verdadeira probabilidade. Intuitivamente é possível conjecturar que à medida que o número de repetições aumenta, as frequências relativas se estabilizam em um número que chamaremos de probabilidade.
Considere dois experimentos: o lançamento de um dado e o lançamento de uma moeda. Considerando que sejam honestos, imaginamos que a probabilidade de uma face qualquer do dado aparecer em um lancamento seja 1/6 (considerando que são 6 faces e todas tem a mesma chance de ocorrência já que o dado é equilibrado). O mesmo para a moeda: considerando que são duas faces, a probabilidade de observar qualquer uma delas é igual a 1/2. Estas suposições são resultantes da atribuição de probabilidades pela forma clássica.
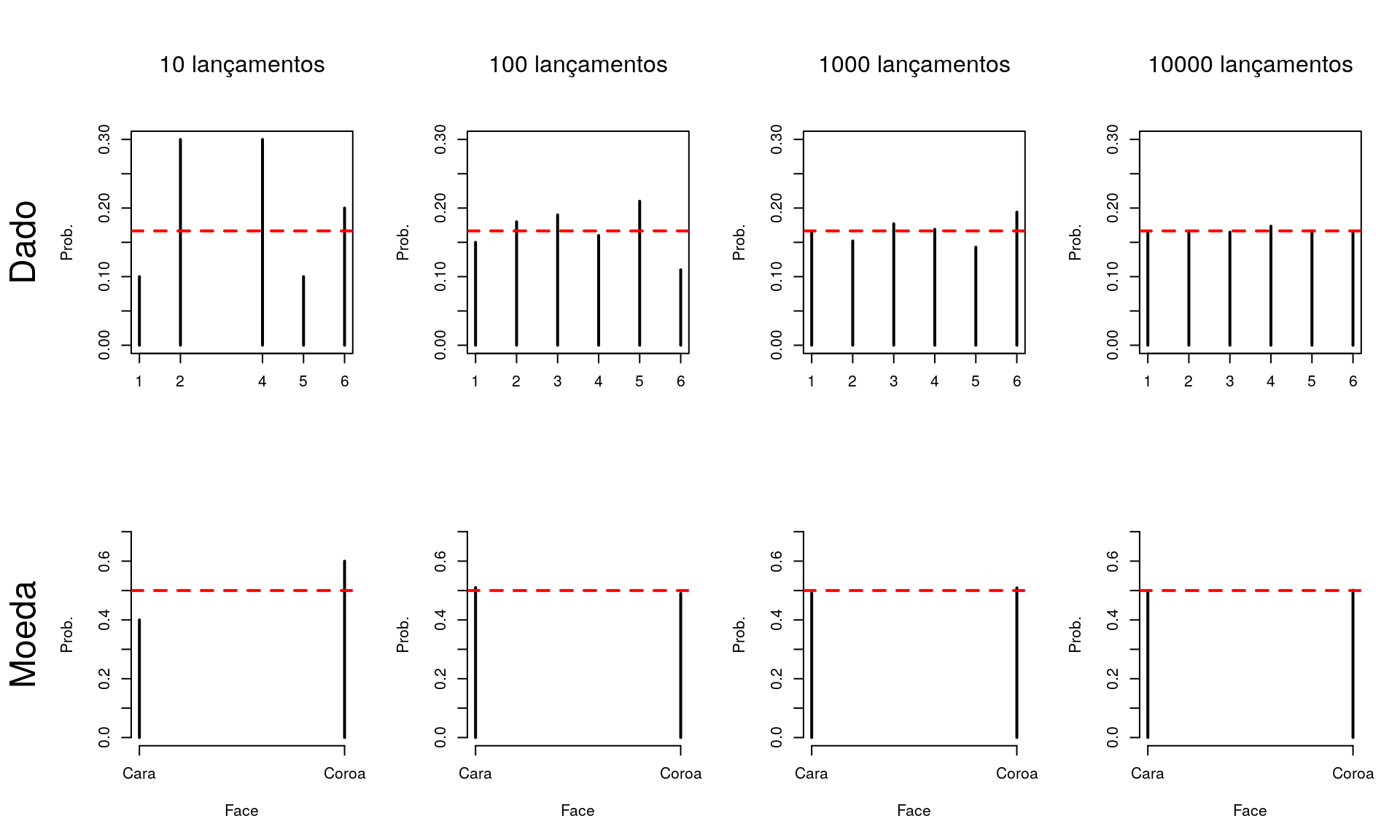
Pela forma frequentista deveríamos repetir o experimento de lançar o dado e a moeda um grande número de vezes já que a Lei dos Grandes Números nos diz que as estimativas das probabilidades dadas pelas frequências relativas tendem a ficar melhores com mais observações.
Os gráficos a seguir apresentam o resultado da simulação de diversos lançamentos de um dado e uma moeda, note que quanto maior o número de lançamentos mais próxima a probabilidade obtida fica daquela obtida pela forma clássica:
4.1 Adição de probabilidades
A probabilidade da união de eventos é calculada através da regra da adição de probabilidades:
\[P(A ∪ B) = P(A) + P(B) − P(A ∩ B)\]
Se A e B forem disjuntos, a expressão se reduz à soma das probabilidades.
Como consequência da regra da adição, obtemos que, para qualquer evento \(A \subset \Omega\):
\[P(A) = 1 - P(A^{c})\]
Consequentemente:
\[P(A ∪ A^{c}) = P(\Omega) = 1\]
4.2 Probabilidade condidional
Em muitas situações, o fenômeno de interesse pode ser separado em etapas. A informação do que ocorreu em uma etapa pode influenciar nas etapas seguintes. Nestas situações há um ganho de informação e pode-se recalcular as probabilidades. Estas probabilidades são as chamadas probabilidades condicionais. Dados dois eventos A e B, a probabilidade condicional de A ocorrer, dado que ocorreu B é representado por P(A|B).
- Quando \(P(B) > 0\):
\[P(A|B) = \frac{P(A ∩ B)}{P(B)}\]
- Quando \(P(B) = 0\):
\[P(A|B) = P(A)\]
4.3 Regra do produto
Da definição de probabilidade condicional, é possível deduzir a regra do prodto:
\[P({A ∩ B}) = P(A|B)P(B),\] com \(P(B)>0\).
4.4 Independência de eventos
Dois eventos A e B são independentes se a informação da ocorrência de um não altera a probabilidade de ocorrência do outro:
\[P(A|B) = P(A), P(B) > 0\] ou, de forma equivalente:
\[P({A ∩ B}) = P(A)P(B)\]
4.5 Partição do espaço amostral
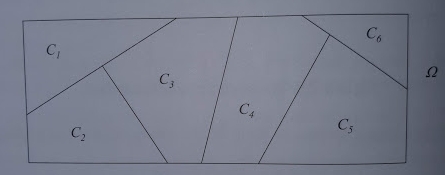
Os eventos \(C_1, C_2, ..., C_k\) formam uma partição do espaço amostral se eles não tem interseção entre si e sua união é igual ao espaço amostral. Isto é:
\(C_i ∩ C_j = \phi\), para \(i \neq j\)
\(∪_{i=1}^{k} C_{i} = \Omega\)
4.6 Teorema de Bayes
Suponha que os eventos \(C_1, C_2, ..., C_k\) formem uma partição de \(\Omega\) e que suas probabilidades sejam conhecidas.Suponha ainda que, para um evento A, se conheçam as probabilidades \(P(A|C_i)\) para todo \(i = 1,2,...,k\). Entãom para qualquer \(j\) temos que:
\[P(C_j|A) = \frac{P(A|C_j)P(C_j)}{\sum_{i=1}^{k}P(A|C_i)P(C_i)},\ j=1,2,...,k\]
Críticas e sugestões a este material sempre serão bem vindas.
Para entrar em contato comigo, envie uma mensagem para lineuacf@gmail.com.