Parte 1 - Conceitos iniciais

1 O que é Estatística

Entende-se por Estatística o conjunto de métodos e técnicas usados para organizar, descrever, analisar e interpretar um ou mais conjuntos de valores (dados) oriundos de estudos e experimentos das mais diversas áreas do conhecimento. Compreende:

Planejamento de coleta de dados (via experimentos ou observação).
Descrição e Análise dos dados para extração de informações.
Interpretação dos resultados a fim de avaliar se estas informações comprovam ou refutam as hipóteses de interesse.

2 Ramos da Estatística

Nos cursos de Estatística básica geralmente são abordadas 3 grandes áreas: Estatística descritiva ou exploratória, Probabilidade e Inferência.

2.1 Estatística descritiva ou exploratória

Conjunto de técnicas destinadas a descrever e resumir dados a fim de tirar conclusões a respeito de características de interesse.

Compreende a etapa de consistência dos dados, isto é, verificar se os dados coletados são condizentes com a realidade.

Nesta etapa busca-se gerar resumos numéricos, medidas descritivas e visualizações gráficas acerca dos dados com o intuito de compreender preliminarmente o comportamento das variáveis individualmente e as interações entre elas.

2.2 Probabilidade

A palavra probabilidade deriva da palavra em Latim probare. A teoria das probabilidades tenta quantificar a noção de provável, ou seja, de que forma podemos lidar e quantificar incertezas.

É a teoria matemática utilizada para se estudar a incerteza oriunda de fenômenos de caráter aleatório.

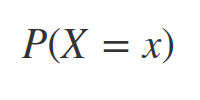
2.3 Inferência

A inferência estatística é o ramo responsável pela estimação de quantidades desconhecidas da população (os chamados parâmetros) com base numa amostra.

Nesta área formulam-se e testam hipóteses com o objetico de extrapolar para a população resultados obtidos na amostra.

Vale ressaltar que se tivermos informação sobre todos os elementos da população não se faz necessário o uso das técnicas de inferência.

3 População e Amostra

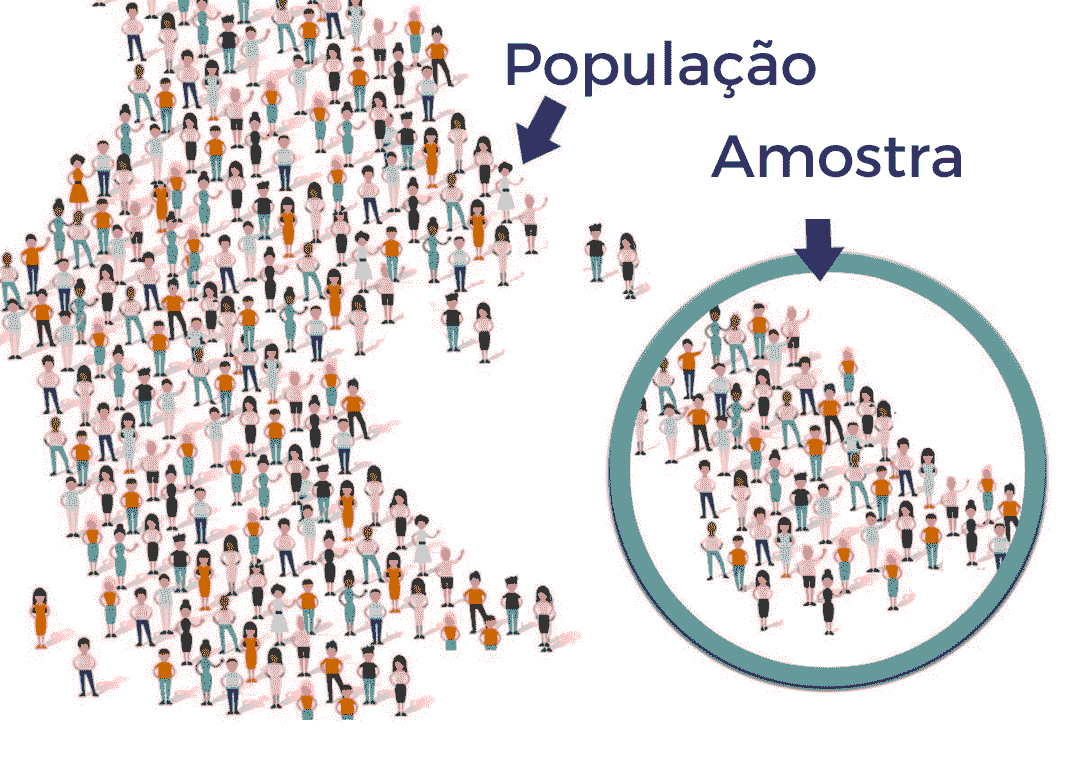
Em Estatística dois conceitos são importatntíssimos: população e amostra.

População: conjunto de seres, itens ou eventos com uma característica comum. TODOS aqueles que possuem a característica de interesse pertencem à população.
Amostra: subconjunto da população. Na prática é inviável trabalhar com a população toda, a alternativa então é trabalhar com uma amostra e inferir os resultados para a população. A seleção da amostra pode ser feita de diversas maneiras. A forma mais comum é a chamada amostragem aleatória simples, em que todos os elementos da população possuem a mesma probabilidade de serem selecionados para a amostra. Existem outras formas de amostragem, tais como: amostragem aleatória estratificada, por agrupamento, sistemática, etc. A forma adequada de amostragem conduz a um menor tamanho amostral para obtenção de uma precisão satisfatória.

4 Etapas do processo de análise

De forma geral, as etapas para análise de um conjunto de dados são:

Definição do problema.
Planejamento do estudo.
Coleta de dados.
Análise dos dados (análise exploratória e aplicação de métodos mais sofisticados que permitam generalizar os resultados para a população).
Interpretação dos resultados.

5 Tabela de dados

Denominam-se Variáveis as características observadas em cada um dos elementos que pertencem à amostra. Na prática precisamos de uma forma para representar indivíduos e variáveis.

Um conjunto de dados considerado arrumado é aquele em que cada coluna representa uma variável, cada linha representa uma observação e cada célula representa o valor observado no elemento \(i\) na variável \(j\):

O conjunto de dados completo e sem tratamentos é denominado conjunto de dados brutos e, na prática, podemos coletar variáveis de diferentes tipos e naturezas.

Como exemplo de conjunto de dados brutos considere que um questionário foi aplicado aos alunos do primeiro ano de uma escola (disponível aqui) e possui as seguintes informações:

Id: identificação do aluno.
Turma: turma a que o aluno foi alocado (A ou B).
Sexo: F se feminino, M se masculino.
Idade: idade em anos.
Alt: altura em metros.
Peso: peso em quilogramas.
Filhos: número de filhos na família.
Fuma: hábito de fumar, sim ou não.
Toler: tolerância ao cigarro: (I) indiferente; (P) incomoda pouco; (M) incomoda muito.
Exerc: horas de atividade física, por semana.
Cine: número de vezes que vai ao cinema por semana.
OpCine: opinião a respeito das salas de cinema na cidade: (B) regular a boa; (M) muito boa.
TV: horas gastas assistindo TV, por semana.
OpTV: opinião a respeito da qualidade da programação na TV: (R) ruim; (M) média; (B) boa; (N) não sabe.

Parte dos dados brutos, representados em forma de tabela têm a seguinte forma:

Informações de questionário estudantil - dados brutos.

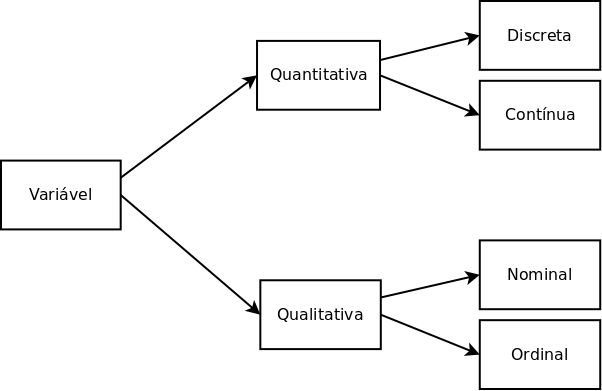
5.1 Tipos de variável

Existem dois tipos de variáveis: as numéricas (quantitativas) e as não numéricas (qualitativas), cada uma das classes tem suas ramificações:

Variáveis Quantitativas: assumem valores numéricos.

Podem ser:

Discretas: características mensuráveis que podem assumir apenas um número finito ou infinito contável de valores e, assim, somente fazem sentido valores inteiros.
Contínuas: características mensuráveis que assumem valores em uma escala contínua, isto é, na reta real.

Variáveis Qualitativas: são as características definidas categorias, ou seja, representam uma classificação dos indivíduos e não uma característica numérica.

Podem ser:

Nominais: não existe ordenação nem peso entre as categorias.
Ordinais: existe uma ordenação entre as categorias.

Existem peculiaridades na classificação de variáveis devido a situações como: discretização de variáveis contínuas, limitações em instrumentos de mensuração, utilização de quantidades numéricas para representação de variáveis categóricas, etc. Deve-se sempre estar atento a este tipo de situação pois podem levar a implicações nas análises e consequentemente nos resultados.

Classificando as variáveis do conjunto de dados do exemplo:

Id: variável qualitativa nominal.
Turma: variável qualitativa nominal.
Sexo: variável qualitativa nominal.
Alt: variável quantitativa contínua.
Peso: variável quantitativa contínua.
Filhos: variável quantitativa discreta.
Fuma: variável qualitativa nominal.
Toler: variável qualitativa ordinal.
Cine: variável quantitativa discreta.
OpCine: variável qualitativa ordinal.
OpTV: variável qualitativa ordinal.

As variáveis Idade, Exerc e TV em essência são variáveis quantitativas contínuas, contudo note como nos dados elas foram tratadas como discretas, tendo em vista que há apenas valores inteiros.

Críticas e sugestões a este material sempre serão bem vindas.

Para entrar em contato comigo, envie uma mensagem para lineuacf@gmail.com.

Noções de Probabilidade e Estatística

`Lineu Alberto`