|
Testes de hipótese em Modelos Multivariados de Covariância Linear Generalizada (McGLM) |
Análise de Variância Multivariada via teste Wald
Lineu Alberto Cavazani de Freitas
Introdução
Como já visto, através da estatística de Wald, podemos realizar testes sobre parâmetros de modelos de regressão e ainda efetuar Análises de Variância dos tipos II e III. Por meio de um procedimento similar, podemos chegar a uma extensão do teste Wald no contexto dos Modelos Multivariados de Covariância Linear Generalizada (McGLM) pois as estimativas dos parâmetros do modelo seguem distribuição Normal.
Sendo assim, podemos chegar a um teste de hipóteses sobre parâmetros de uma classe de modelos que lida com múltiplas respostas não gaussianas, de diferentes naturezas em que modela-se também a correlação entre indivíduos da amostra.
Do mesmo modo que é feito para um modelo univariado, podemos chegar também a uma Análise de Variância Multivariada (MANOVA) realizando sucessivos testes do tipo Wald em que estamos interessados em avaliar o efeito de determinada variável nas \(R\) respostas simultaneamente. Portanto, a pergunta que a ser respondida seria: esta variável tem efeito diferente de 0 para todas as respostas?
A MANOVA clássica (Smith, Gnanadesikan, and Hughes 1962) é um assunto com vasta discussão na literatura e possui diversas propostas com o objetivo de verificar a nulidade dos parâmetros de um modelo de regressão multivariado, como o lambda de Wilk’s (Wilks 1932), traço de Hotelling-Lawley (Lawley 1938; Hotelling 1951), traço de Pillai (Pillai and others 1955) e maior raiz de Roy (Roy 1953). No entanto, considerando um cenário com múltiplas respostas não gaussianas, tal como é permitido no contexto do McGLM, são escassas as discussões na literatura a respeito de testes de hipóteses sobre os parâmetros do modelo.
Neste material serão tratados os seguintes assuntos:
Teste Wald para o McGLM: suposições, hipóteses, estatística de teste e distribuição da estatística de teste.
Análises de Variância multivariada via teste Wald: procedimento para obtenção de um quadro de Análise de Variância Multivariada obtido por sucessivos testes do tipo Wald sobre os parâmtros de um McGLM.
Teste Wald multivariado
Tal como no cenário univariado, as hipóteses de interesse são:
\[H_0: \boldsymbol{L\beta = c} \ vs \ H_1: \boldsymbol{L\beta} \neq c.\]
Neste cenário, considerando múltiplas respostas, a matriz \(\boldsymbol{L}\) é o produto Kronecker de duas matrizes: uma matriz \(\boldsymbol{G}\) e uma \(\boldsymbol{F}\), ou seja, \(\boldsymbol{L}\) = \(\boldsymbol{G} \otimes \boldsymbol{F}\). A matriz \(\boldsymbol{G}\) tem dimensão \(R \times R\) e especifica as hipóteses referentes às respostas, já a matriz \(\boldsymbol{F}\) especifica as hipóteses entre variáveis e tem dimensão \(s \times p\), em que \(s\) é o número de restrições lineares, ou seja, o número de parâmetros testados, e \(p\) é o número total de coeficientes de regressão do modelo. Portanto, a matriz \(\boldsymbol{L}\) tem dimensão (\(sR \times p\)). \(\boldsymbol{\beta}\) é o vetor empilhado dos parâmetros de regressão das \(R\) respostas, tem dimensão \(p \times 1\). E \(\boldsymbol{c}\) é um vetor de valores a serem confrontados com as estimativas originais do modelo, de dimensão \(sR \times 1\). É simples verificar a compatibilidade das matrizes.
Em geral, a matriz \(\boldsymbol{G}\) é uma matriz identidade de dimensão igual ao número de respostas analisadas no modelo. Enquanto que a matriz \(\boldsymbol{F}\) tem o mesmo formato da matriz \(\boldsymbol{L}\) do caso caso univariado. Utilizamos o produto Kronecker (\(\otimes\)) destas duas matrizes (\(\boldsymbol{G}\) e \(\boldsymbol{F}\)) para que a hipótese descrita na matriz \(\boldsymbol{F}\) seja testada simultaneamente para as \(R\) respostas do modelo, ou seja, podemos testar se um parâmetro referente a uma variável presente nas múltiplas respostas é igual a um valor estipulado. Em geral, tal como no caso univariado, as hipóteses giram em torno de vetores nulos a fim de verificar se há efeito daquela variável. Contudo, no caso multivariado, verificamos se há efeito de determinada variável em todas as respostas ao mesmo tempo.
Exemplo
Para fins de ilustração, considere um modelo com duas variáveis resposta e preditor dado por:
\[g_r(\mu_r) = \beta_{r0} + \beta_{r1} x_1 + \beta_{r2} x_2\]
Hipóteses para um parâmetro
Podemos estar interessados em testar se um único parâmetro, comum a todas as respostas, é igual a um valor postulado, por exemplo:
\[H_0: \beta_{r1} = 0 \ vs \ H_1: \beta_{r1} \neq 0.\]
Ou, da mesma forma:
\[H_0: \begin{pmatrix} \beta_{11} \\ \beta_{12} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \ vs \ H_1: \begin{pmatrix} \beta_{11} \\ \beta_{12} \end{pmatrix} \neq \begin{pmatrix} 0 \\ 0 \end{pmatrix}.\]
Ou seja, estaríamos verificando se há evidência suficiente para afirmar que o parâmetro \(\beta_1\) é igual a 0 em ambas as respostas.
Esta mesma hipótese pode ser escrita na notação genérica \(\boldsymbol{L\beta} = \boldsymbol{c}\):
\[H_0: \boldsymbol{L\beta} = \boldsymbol{c} \ vs \ H_1: \boldsymbol{L\beta} \neq \boldsymbol{c}.\]
Sendo assim:
\(\boldsymbol{G}\) = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), uma matriz identidade 2x2, pois temos 2 respostas.
\(\boldsymbol{F}\) = \(\begin{bmatrix} 0 & 1 & 0 \end{bmatrix}\), uma matriz 1x3, que especifica o parâmetro a ser testado. Neste caso é o \(\beta_1\) de cada resposta \(R\).
\(\boldsymbol{L}\) = \(\boldsymbol{G} \otimes \boldsymbol{F}\), uma matriz 2x6 que especifica a hipótese a ser testada no vetor empilhado de parâmetros de regressão de ambas as respostas. Ou seja:
\[\boldsymbol{L} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}\]
\(\boldsymbol{\beta}\) = \(\begin{bmatrix} \beta_{10}\\ \beta_{11}\\ \beta_{12}\\ \beta_{20}\\ \beta_{21}\\ \beta_{22} \end{bmatrix}\), um vetor com os parâmetros de regressão das duas respostas, empilhadas. Tem dimensão 6x1.
\(\boldsymbol{c}\) = \(\begin{bmatrix} 0 \\ 0 \end{bmatrix}\), um vetor 2x1.
Note que as dimensões são compatíveis e o resultado do produto é a mesma hipótese já enunciada:
\[H_0: \beta_{r1} = 0 \ vs \ H_1: \beta_{r1} \neq 0.\]
Hipóteses para múltiplos parâmetros
Considerando o mesmo preditor, podemos estar interessados em testar mais de um parâmetro ao mesmo tempo, por exemplo:
\[H_0: \begin{pmatrix} \beta_{r1} \\ \beta_{r2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \ vs \ H_1: \begin{pmatrix} \beta_{r1} \\ \beta_{r2} \end{pmatrix} \neq \begin{pmatrix} 0 \\ 0 \end{pmatrix}.\]
Ou ainda:
\[H_0: \begin{pmatrix} \beta_{11} \\ \beta_{12} \\ \beta_{21} \\ \beta_{22} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \ vs \ H_1: \begin{pmatrix} \beta_{11} \\ \beta_{12} \\ \beta_{21} \\ \beta_{22} \end{pmatrix} \neq \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}.\]
Neste caso, teríamos interesse em verificar se, simultâneamente, os parâmetros \(\beta_1\) e \(\beta_2\) são iguais a 0 para ambas as respostas.
Na notação genérica \(\boldsymbol{L\beta} = \boldsymbol{c}\), temos as hipóteses:
\[H_0: \boldsymbol{L\beta} = \boldsymbol{c} \ vs \ H_1: \boldsymbol{L\beta} \neq \boldsymbol{c}.\]
Em que:
\(\boldsymbol{G}\) = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), uma matriz identidade 2x2, pois temos 2 respostas.
\(\boldsymbol{F}\) = \(\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\), uma matriz 2x3, que especifica os parâmetros a serem testados. Neste caso: \(\beta_1\) e \(\beta_2\) de cada resposta \(R\).
\(\boldsymbol{L}\) = \(\boldsymbol{G} \otimes \boldsymbol{F}\), uma matriz 4x6 que especifica a hipótese a ser testada no vetor empilhado de parâmetros de regressão de ambas as respostas. Ou seja:
\[\boldsymbol{L} = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1\end{bmatrix}\]
\(\boldsymbol{\beta}\) = \(\begin{bmatrix} \beta_{10}\\ \beta_{11}\\ \beta_{12}\\ \beta_{20}\\ \beta_{21}\\ \beta_{22} \end{bmatrix}\), um vetor com os parâmetros de regressão das duas respostas, empilhadas. Tem dimensão 6x1.
\(\boldsymbol{c}\) = \(\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\), um vetor 4x1.
Note que as dimensões são compatíveis e o resultado do produto é a mesma hipótese já enunciada.
Em geral, tal como no caso univariado, ao realizar este tipo de teste há interesse em confrontar o valor dos parâmetros estimados com 0 para verificar se existe efeito das variáveis no modelo, contudo podem ser utilizados outros valores diferentes de 0.
Estatística de teste
Seja \(\boldsymbol{\hat{\theta}} = (\boldsymbol{\hat{\beta}^{\top}}, \boldsymbol{\hat{\lambda}^{\top}})^{\top}\) o estimador dos parâmetros de um McGLM, sabemos que:
\[\begin{equation} \begin{aligned} \boldsymbol{\hat{\theta}} \sim N(\boldsymbol{\theta}, J_{\boldsymbol{\theta}}^{-1}), \end{aligned} \end{equation}\]
Ou seja, temos o suficiente para generalizar o existente e conhecido teste de Wald para testar hipóteses sobre parâmetros de um McGLM, pois as estimativas dos parâmetros seguem distribuição Normal e podemos obter o erro padrão pela matriz de informação de Godambe. Para avaliar a hipótese faz-se uso da estatística de Wald dada por:
\[ W = \left (\boldsymbol{L\hat{\beta} - c} \right )^T\left ( \boldsymbol{LJ_{\beta}^{-1} L^T} \right )^{-1}\left (\boldsymbol{L\hat{\beta} - c} \right ), \]
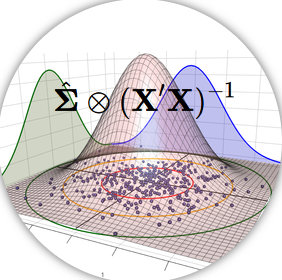
em que \(\boldsymbol{J_{\boldsymbol{\beta}}^{-1}}\) é a parte da inversa da matriz de informação de Godambe que considera apenas os parâmetros de regressão, ou seja, é a matriz de variância e covariância dos parâmetros de regressão de um McGLM.
Sob a hipótese nula, a estatística segue assintoticamente distribuição Qui-quadrado com \(sR\) graus de liberdade e é possível notar que essa construção permite realizar o teste de hipóteses para todas as variáveis resposta, bem como entre combinações de variáveis e todos os possíveis contrastes entre os níveis de tratamento.
Análise de Variância Multivariada via teste Wald
Como já visto, as Análises de Variância são sucessivos testes de hipótese que consideram a nulidade de determinados parâmetros a fim de verificar se sua ausência gera perda ao modelo ou, em outras palavras, se existe efeito da variável explicativa na variável resposta.
No cenário com múltiplas respostas isto segue sendo feito através de uma sequência de testes que podem ser efetuados utilizando a estatística de Wald. Mais especificamente, é possível desenvolver Análises de Variância do tipo II e III para modelos multivariados que comportam respostas não gaussianas.
Do mesmo modo que no caso univariado, basta, para cada linha do quadro de Análise de Variância, especificar uma matriz \(\boldsymbol{L}\) que represente de forma adequada a hipótese a ser testada para todas as respostas.
Exemplo
Para ilustração das hipóteses que seriam testadas via teste Wald em cada linha do quadro de Análise de Variância nos tipos II e III para um modelo multivariado, considere um modelo qualquer, com 2 variáveis resposta com preditor dado por:
\[g_r(\mu_r) = \beta_{r0} + \beta_{r1} x_1 + \beta_{r2} x_2 + \beta_{r3} x_3 + \beta_{r4} x_1 x_2.\]
Temos deste modo, para cada resposta: um intercepto, denotado por \(\beta_0\) e quatro parâmetros de regressão denotados por \(\beta_1\), \(\beta_2\) e \(\beta_3\) e \(\beta_4\), em que \(\beta_4\) representa o efeito da interação entre as variáveis \(x_1\) e \(x_2\).
Como se trata de um modelo com 2 variáveis resposta, a matriz \(\boldsymbol{G}\) é uma identidade de ordem 2, ou seja:
\[\boldsymbol{G} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}.\]
A matriz \(\boldsymbol{G}\) é fixa, contudo a matriz \(\boldsymbol{F}\) varia a cada linha do quadro de Análise de Variância pois é na matriz \({F}\) que são especificados quais parâmetros serão testados; portanto variam conforme a natureza das variáveis (qualitativas ou quantitativas) e do tipo de Análise de Variância (II ou III).
MANOVA tipo II
Sendo assim temos, para o tipo II as seguintes hipóteses seriam testadas:
Na primeira linha, referente a \(x_1\), testaríamos o modelo completo contra o modelo sem todos os parâmetros que possuem \(x_1\), sejam fixos ou interações e independente da resposta, portanto:
\[H_0: \begin{pmatrix} \beta_{r1} \\ \beta_{r4} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \ vs \ H_1: \begin{pmatrix} \beta_{r1} \\ \beta_{r4} \end{pmatrix} \neq \begin{pmatrix} 0 \\ 0 \end{pmatrix}.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}\]
Tal como a variável \(x_1\), \(x_2\) está associado a um efeito de interação, portanto ambos efeitos (fixo e interação) são testados. A segunda linha do quadro, referente a \(x_2\), testaria as hipóteses:
\[H_0: \begin{pmatrix} \beta_{r2} \\ \beta_{r4} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \ vs \ H_1: \begin{pmatrix} \beta_{r2} \\ \beta_{r4} \end{pmatrix} \neq \begin{pmatrix} 0 \\ 0 \end{pmatrix}.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}\]
A terceira linha do quadro testaria uma única hipótese, pois o parâmetro \(x_3\) não está associado a nenhum outro efeito:
\[H_0: \beta_{r3} = 0 \ vs \ H_1: \beta_{r3} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}\]
Por fim, a última linha do quadro testaria o efeito da interação no modelo, ou seja:
\[H_0: \beta_{r4} = 0 \ vs \ H_1: \beta_{r4} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}\]
A partir de cada matriz \(F\) é gerada uma matriz \(L\) dada pelo produto Kronecker \(G \otimes F\). Para cada matriz \(L\) é obtido o valor da estatística de teste \(W\) bem como um p-valor associado e o resultado final é sumarizado num quadro de Análise de Variância Multivariada que permite, de forma simples, avaliar se determinada variável tem ou não efeito a todas as resposta.
MANOVA tipo III
Tal como no caso univariado a Análise de Variância Multivariada do tipo III não trata de forma distinta efeitos fixos de interações. Os testes em cada linha do quadro seriam:
Na primeira linha, referente a \(x_1\), testaríamos o modelo completo contra o modelo sem \(x_1\).
\[H_0: \beta_{r1} = 0 \ vs \ H_1: \beta_{r1} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 1 & 0 & 0 & 0 \\ \end{bmatrix}\]
Na segunda linha, referente a \(x_2\), testaríamos o modelo completo contra o modelo sem \(x_2\). Tal como para \(x_1\), na análise do tipo III nada se supõe quanto ao parâmetro de interação, por mais que lá haja \(x_2\):
\[H_0: \beta_{r2} = 0 \ vs \ H_1: \beta_{r2} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ \end{bmatrix}\]
O mesmo para a terceira linha:
\[H_0: \beta_{r3} = 0 \ vs \ H_1: \beta_{r3} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}\]
Por fim, a última linha do quadro testaria o efeito da interação no modelo, ou seja, testa o modelo completo contra o modelo sem interação:
\[H_0: \beta_{r4} = 0 \ vs \ H_1: \beta_{r4} \neq 0.\]
O que resulta em uma matriz \(F\) com a seguinte forma:
\[F = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}\]
Do mesmo modo que na análise do tipo II, é gerada uma matriz \(L\) e para cada matriz \(L\) é obtido o valor da estatística de teste \(W\) e um p-valor associado.
No caso de variáveis categóricas, são estimados o número de categorias menos um parâmetros. Neste caso, a matriz \(F\) deve ser corretamente espeficicada para testar todos os parâmetros associados a níveis de determinada variável categórica.
Além disso, através do mesmo procedimento podemos extender os testes para comportar parâmetros de dispersão e potência de tal modo que seja possível avaliar o efeito da correlação entre os indivíduos e ainda verificar que distribuição de probabilidade conhecida se adequa bem ao problema de acordo com a função de variância utilizada.

|

|