Primeiros Passos com o R

Lineu Alberto

Parte 3 - Importação e Programação

1 Leitura de dados

Existem duas formas de trabalhar com leitura de dados no R: na primeira delas o usuário digita os dados e armazena num objeto, na segunda o usuário lê um arquivo externo (na memória do computador ou até mesmo algum arquivo disponível online).

A primeira já foi suficientemente discutida quando foram apresentadas as funções c(), rep(), seq(), matrix(), data.frame(), list(), etc. Além dessas, são opções interessantes as funções scan() e readLines().

Já para o caso de leitura de arquivos externos, os formatos mais comuns de arquivos para leitura são: texto (txt), comma separated values (csv) e planilhas Excel (xlsx). Todos estes formatos podem ser importados para o R. Outros formatos também são possíveis, mas abordaremos apenas estes por serem os mais comuns.

Contudo, para que a importação seja feita de forma adequada há a necessidade de que os dados estejam tabulados e organizados de forma correta, isto é: observações nas LINHAS, variáveis nas COLUNAS e cada coluna representando uma única variável.

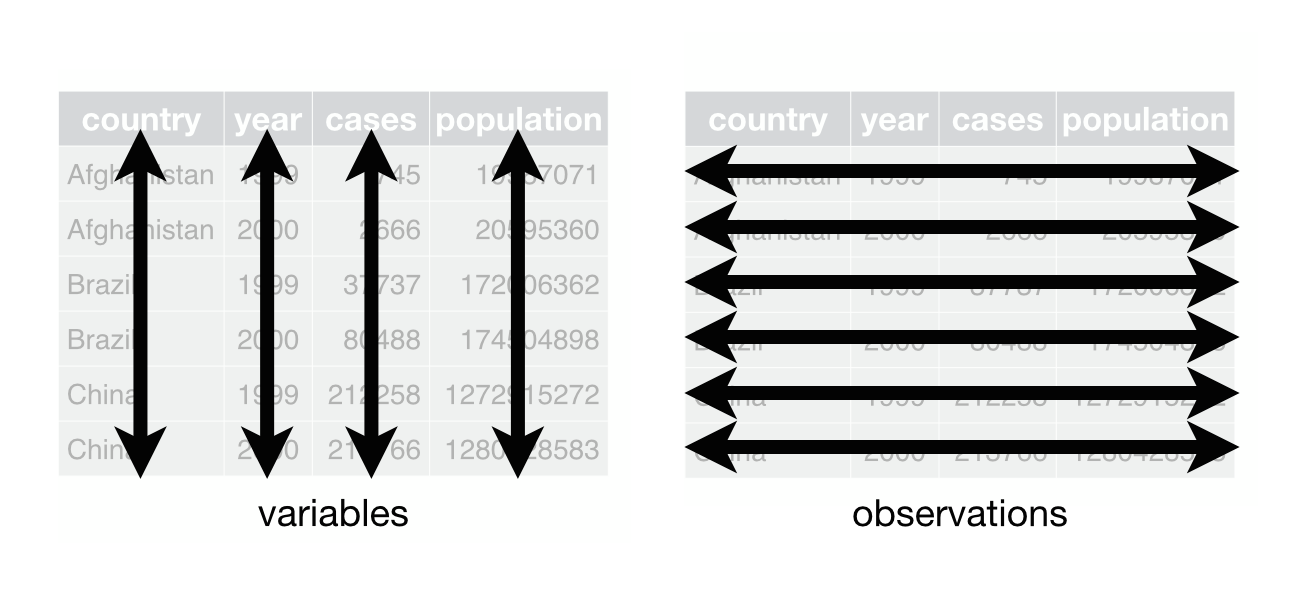
Existem diversos pacotes e funções para importação de dados, as 3 a seguir são apenas opções:

  • Leitura de arquivos .txt: read.table().
  • Leitura de arquivos .csv: read.csv().
  • Leitura de arquivos .xlsx: gdata::read.xls().

Em geral, a leitura de arquivos externos gera um data frame e cabe ao usuário verificar se os dados possuem cabeçalho, qual o formato dos dados, separador, decimal e dentre outras informações para correta leitura dos dados no R. Além disso, após a leitura, é de suma importância verificar se os formatos das variáveis foram interpretados corretamente e, caso não tenham sido, convertê-las (em geral fazendo uso das funções do tipo as. já discutidas).

Lembre-se de ler a documentação da função a fim de compreender a utilização dos argumentos para especificá-los de modo que a leitura dos dados seja feita de forma correta. Vejamos um exemplo para cada formato:

1.1 txt

##   emp grp    x1    x2   x3   x4
## 1   1   1 -0.45 -0.41 1.09 0.45
## 2   2   1 -0.56 -0.31 1.51 0.16
## 3   3   1  0.06  0.02 1.01 0.40
## 4   4   1 -0.07 -0.09 1.45 0.26
## 5   5   1 -0.10 -0.09 1.56 0.67
## 6   6   1 -0.14 -0.07 0.71 0.28

1.2 csv

##   emp grp    x1    x2   x3   x4
## 1   1   1 -0.45 -0.41 1.09 0.45
## 2   2   1 -0.56 -0.31 1.51 0.16
## 3   3   1  0.06  0.02 1.01 0.40
## 4   4   1 -0.07 -0.09 1.45 0.26
## 5   5   1 -0.10 -0.09 1.56 0.67
## 6   6   1 -0.14 -0.07 0.71 0.28

1.3 xlsx

##   emp grp    x1    x2   x3   x4
## 1   1   1 -0.45 -0.41 1.09 0.45
## 2   2   1 -0.56 -0.31 1.51 0.16
## 3   3   1  0.06  0.02 1.01 0.40
## 4   4   1 -0.07 -0.09 1.45 0.26
## 5   5   1 -0.10 -0.09 1.56 0.67
## 6   6   1 -0.14 -0.07 0.71 0.28

2 Programação

Através da programação é possível automatizar processos, isto é, tarefas que seriam feitas manualmente por seres humanos passam a ser realizadas total ou parcialmente pelo computador. A sequência de passos a ser seguida para realização de uma tarefa é chamada de algoritmo. Para que o computador realize esta sequência de passos é necessário que isso esteja especificado de uma forma que a máquina entenda, isto é, através de uma linguagem de programação.

As estruturas existentes nas linguagens são as mesmas e, por este motivo, é interessante compreender bem estas estruturas de forma genérica para que seja mais simples generalizá-las para diferentes linguagens de programação.

Entenda: é mais fácil você aprender a lógica (que é geral e genérica) antes da linguagem (que é única e segue padrões próprios).

Leia o post Algoritmos e Lógica de Programação.

Vamos discutir como as estruturas genéricas, isto é, presentes em qualquer linguagem de programação, funcionam em R.

Alguns dos tópicos importantes já foram vistos quando as estruturas de dados em R foram apresentadas, como os operadores aritméticos (soma, subtração, divisão, etc), os operadores relacionais (maior, menor, igual, etc) e operadores lógicos (e, ou e não). Mas vamos passar por eles novamente a fim de varrer todas as ferramentas necessárias para fins de programação.

2.1 Operadores aritiméticos

Os operadores aritméticos servem para realizar operações matemáticas básicas. As representações das operações básicas em R são:

Operador Operação
+ Adição
- Subtração
* Multiplicação
/ Divisão
^ Potência
exp() Exponencial
sqrt() Raiz quadrada
factorial() Fatorial
log() Logaritmo
abs() Valor absoluto
round() Arredondamento
ceiling() Arredondamento para cima
floor() Arredondamento para baixo

Os operadores seguem uma hierarquia, ou seja, uma ordem de precedência. Inicialmente são efetuadas as operações entre parênteses seguindo a ordem: exponenciação, multiplicação/divisão e por fim adição/subtração.

2.2 Operadores relacionais

Os operadores relacionais são utilizados para comparar valores de variáveis e sempre retornam valores lógicos, ou seja, verdadeiro ou falso. No R os operadores relacionais são:

Operador Operação
> Maior que
< Menor que
>= Maior ou igual que
<= Menor ou igual que
== Igual
!= Diferente

2.3 Operadores lógicos

Os operadores lógicos, assim como os relacionais, retornam resultados lógicos. Contudo sua finalidade é outra. Diferentemente dos aritméticos eles servem para comparar outros resultados lógicos. Existem 3 operadores lógicos: E, OU e NÃO; representados no R por &,| e !, respectivamente.

Os operadores lógicos são os últimos da hierarquia de precedência, pois inicialmente são efetuadas as operações aritméticas, depois as relacionais e, por fim, as operações lógicas.

2.4 Estruturas condicionais

Uma estrutura condicional é utilizada quando a ação a ser tomada depende de uma condição ser ou não satisfeita, algo como: se tal coisa acontecer faça isso, senão faça aquilo.

Podemos trabalhar com condicionais simples, compostas e aninhadas. Há ainda uma estrutura condicional chamada estrutura de escolha:

2.4.1 Condicional simples

Quando uma ação é tomada apenas se a condição de interesse for verdadeira. Genericamente:

Considere que estamos interessados em verificar se um valor armazenado em uma variável x é maior que 100.

## [1] "Este número é maior que 100"

Note como no caso acima caso o valor não seja maior que 100 nenhuma ação será tomada.

2.4.2 Condicional composta

Quando uma ação é tomada quando a condição de interesse for verdadeira e outra for tomada quando ela for falsa. Genericamente:

Consideremos o mesmo exemplo anterior, mas agora estamos interessados em retornar duas mensagens diferentes: uma para caso o número seja maior que 100 e outra para caso não seja:

## [1] "Este número NÃO é maior que 100"

2.4.3 Condicional aninhada

Quando há mais de uma situação. Neste caso necessitamos de diversas condicionais, uma dentro da outra. Genericamente:

Desta forma podemos ampliar o exemplo anterior adicionando mais uma condição:

## [1] "Este número é IGUAL a 100"

2.4.4 Estrutura de escolha

A estrutura de escolha é uma opção bem mais simples que a solução de condicionais aninhadas. Genericamente:

Para construção de uma sentença utilizando switch() podemos fazer uso dos índices:

## [1] "segunda mensagem"

Também é possível utilizar o switch() com o valor que a variável analisada assume:

## [1] 1

2.5 Estruturas de repetição

As estruturas de repetição permitem executar mais de uma vez um mesmo bloco de código sob determinadas condições quantas vezes forem necessárias. Por se tratar de uma ou mais operações que se repetem, também são chamadas de laços interativos ou loops. Temos 3 ferramentas para construir loops no R: o enquanto, o repita e o para.

2.5.1 Enquanto

A primeira forma de se utilizar uma estrutura de repetição é com o enquanto, de tal forma que dizemos: “enquanto a condição não for aceita faça tal coisa”. Normalmente a condição está associada a um contador. Genericamente:

Um exemplo simples:

## [1] 3
## [1] 5
## [1] 7
## [1] 9
## [1] 11
## [1] 13
## [1] 15

2.5.2 Repita

É uma estrutura extremamente parecida com o enquanto, porém é logicamente inversa. Trata-se de uma estrutura alternativa ao enquanto em que o teste lógico é feito no final da estrutura, e não no começo. Compare:

  • Enquanto a condição não for aceita faça tal coisa.

  • Faça tal coisa até que a condição seja aceita.

No R essa estrutura sempre vem acompanhada de um if e um break para que o loop seja encerrado. Genericamente:

Um exemplo simples:

## [1] 2
## [1] 4
## [1] 6
## [1] 8
## [1] 10
## [1] 12
## [1] 14
## [1] 16
## [1] 18
## [1] 20
## [1] 22
## [1] 24
## [1] 26
## [1] 28
## [1] 30

2.5.3 Para

O para é uma das estruturas mais utilizadas e possui uma vantagem sobre as outras duas apresentadas: ela é auto incrementável, isto é, não há necessidade de especificar que uma variável contadora recebe ela mesma mais um incremento, o para faz isso automaticamente o que exige menos código para realização de uma tarefa que exige repetição. Genericamente:

Um exemplo simples:

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

2.5.4 Extra

Existe uma função no R chamada ifelse() que pode facilitar as tarefas em algumas situações, verifique.

Existe um operador chamado next que pode ser utilizado quando desejamos que uma iteração seja ignorada e que a próxima seja executada normalmente, por exemplo, caso estejamos interessados em printar em tela os números de 1 a 10 EXCETO 5 e 7:

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 6
## [1] 8
## [1] 9
## [1] 10

O break, apresentado na estrutura repeat pode ser usado para forçar a parada de outros loops, veja:

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7

3 Família apply

A família apply é um conjunto de funções que servem como alternativa aos loops em R. São úteis para melhorar o fluxo de trabalho e reduzir o tempo computacional. As mais utilizadas são: apply, tapply, laaply, sapply. Outras menos utilizadas são: mapply, eapply, rapply, etc.

3.1 apply

Utiliza-se a apply quando temos uma matriz ou um dataframe e desejamos aplicar a mesma função a todas as linhas ou todas as colunas.

X = matriz ou dataframe, MARGIN = 1 para cálculos em linhas; 2 para cálculos em colunas, FUN = função a ser aplicada.

Vamos aplicar a função apply a uma matriz:

  • Gerando uma matriz 4x4:
##      [,1] [,2] [,3] [,4]
## [1,]   14    7    2   12
## [2,]    4    7   11    4
## [3,]    0   14    1    0
## [4,]    0    5   11   13
  • Obtendo a média das linhas:
## [1] 8.75 6.50 3.75 7.25
  • Obtendo a média das colunas:
## [1] 4.50 8.25 6.25 7.25

3.2 tapply

Com a tapply é possível obter medidas descritivas de variáveis para cada nível de uma outra variável disponível nos dados.

X = coluna de uma matriz ou dataframe que será utilizada para fazer os cálculos, INDEX = é a coluna de uma matriz ou dataframe que contém os níveis, FUN = função a ser aplicada.

Vamos considerar o dataset iris nativo do R e obter a média da variável Sepal.Length para cada nível da variável Species:

##     setosa versicolor  virginica 
##      5.006      5.936      6.588

3.3 laaply e sapply

O laaply e a sapply são usadas quando temos uma lista e queremos aplicar a mesma função a cada elemento da lista. Utilizando a laapply o resultado será uma lista já o resultado da sapply será um vetor.

X = é uma lista, FUN = função a ser aplicada em cada elemento da lista.

Considere o conjunto de dados nativo do R women. Este data set é um data frame tem duas variávais: height e weight.

  • Vamos convertê-lo em uma lista:
## $height
##  [1] 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
## 
## $weight
##  [1] 115 117 120 123 126 129 132 135 139 142 146 150 154 159 164
  • E obter a média para cada elemento da lista pelas duas formas:
## $height
## [1] 65
## 
## $weight
## [1] 136.7333
##   height   weight 
##  65.0000 136.7333

Recomendo fortemente a leitura dos seguintes materiais, os quais usei como base para produção desse texto:

Críticas e sugestões a este material sempre serão bem vindas.

Para entrar em contato comigo, envie uma mensagem para .