\[\textbf{Lineu Alberto Cavazani de Freitas}\] \[\textbf{Prof. Cesar Augusto Taconeli}\] \[\textbf{Modelos Lineares Generalizados (CE225)}\]

Modelos de Regressão para Dados de Contagem

Número de Acidentes de Trânsito em Municípios do Paraná em 2010

1 Dados

Os dados extraídos da base de dados pública do Ipardes e dizem respeito ao número de acidentes de trânsito em municípios do Paraná no ano de 2010. O Batalhão de Polícia de Trânsito - BPTRAN define como acidente de trânsito todo evento ocorrido na via pública, inclusive calçadas, decorrente do trânsito de veículos e pessoas, que resulta em danos humanos e materiais.

Compreende: colisões entre veículos, choque com objetos fixos, capotamentos, tombamentos, atropelamentos, queda de pedestres e ciclistas, etc. Além disso toda ocorrência fortuita ou danosa, envolvendo veículos em circulação, ou parados, respectivos ocupantes, pedestres e objetos móveis ou fixos.

Os dados consideram apenas os acidentes de trânsito ocorridos nas vias municipais (não foram incluídos acidentes ocorridos nas Rodovias Estaduais e Federais).

Cada linha da base diz respeito a 1 dos 399 municípios do estado do Paraná, foram coletadas as variáveis:

actt - Número de acidentes de trânsito no município

pibpc - Produto Interno Bruto per Capita do município.

ater - Área Territorial (km²).

gurb - Grau de Urbanização, percentagem da população da área urbana em relação à população total.

frvei - Frota total de veículos.

pop - População Censitári.

O objetivo da análise foi modelar o número de acidentes de trânsito em função das demais variáveis.

ipardes  <- read.csv2('consulta.csv', header = T, sep = ';', dec = ',')

As primeiras 6 linhas da base de dados tem a seguinte forma:

head(ipardes)

##                   cidade actt pibpc     ater  gurb frvei    pop
## 1              Abati\xe1   18 10414  227.898 73.83  2332   7764
## 2        Adrian\xf3polis   NA 10680 1341.334 32.31  1549   6376
## 3          Agudos do Sul    6 10535  191.282 34.12  3142   8270
## 4 Almirante Tamandar\xe9  190  6850  191.114 95.82 33697 103204
## 5  Altamira do Paran\xe1    1  8683  387.315 49.58  1101   4306
## 6        Alto Para\xedso    1 11468 1045.718 55.27  1053   3206

2 Análise Descritiva

Vamos realizar uma breve análise descritiva dos dados.

2.1 Medidas Resumo

Usando a função summary vamos verificar o mínimo, o máximo, a mediana e os quartis das variáveis explicativas em estudo:

summary(ipardes)

##   cidade                           actt             pibpc       
##  \xc2ngulo             :  1   Min.   :    1.0   Min.   :  6305  
##  Abati\xe1             :  1   1st Qu.:    6.0   1st Qu.: 10285  
##  Adrian\xf3polis       :  1   Median :   21.0   Median : 12919  
##  Agudos do Sul         :  1   Mean   :  234.8   Mean   : 15074  
##  Almirante Tamandar\xe9:  1   3rd Qu.:   69.5   3rd Qu.: 16864  
##  Alt\xf4nia            :  1   Max.   :25109.0   Max.   :197335  
##  (Other)               :393   NA's   :44                        
##       ater              gurb            frvei              pop         
##  Min.   :  61.14   Min.   :  9.35   Min.   :    367   Min.   :   1409  
##  1st Qu.: 214.45   1st Qu.: 55.27   1st Qu.:   1766   1st Qu.:   5037  
##  Median : 351.12   Median : 71.90   Median :   3447   Median :   9026  
##  Mean   : 500.95   Mean   : 68.39   Mean   :  12636   Mean   :  26177  
##  3rd Qu.: 624.38   3rd Qu.: 84.22   3rd Qu.:   7264   3rd Qu.:  17274  
##  Max.   :3177.60   Max.   :100.00   Max.   :1197974   Max.   :1751907  
##

Na variável cidade são elencados todos os municípios do Paraná. Para a variável resposta (número de acidentes de trânsito) nota-se um número considerável de dados faltantes; em 44 municípios não há, por algum motivo, o número de acidentes de trânsito. Para as demais variáveis é evidente a grande amplitude das respostas observadas.

2.2 Boxplots

O boxplot é uma alternativa de análise descritiva para avaliação da distribuição dos dados.

par(mfrow=c(2,3))

for (i in 2:ncol(ipardes)) {
  boxplot(ipardes[,i], 
          xlab = '', 
          ylab = '', 
          main = names(ipardes[i]), 
          las=1,
          col = '#C8F9F3')
}

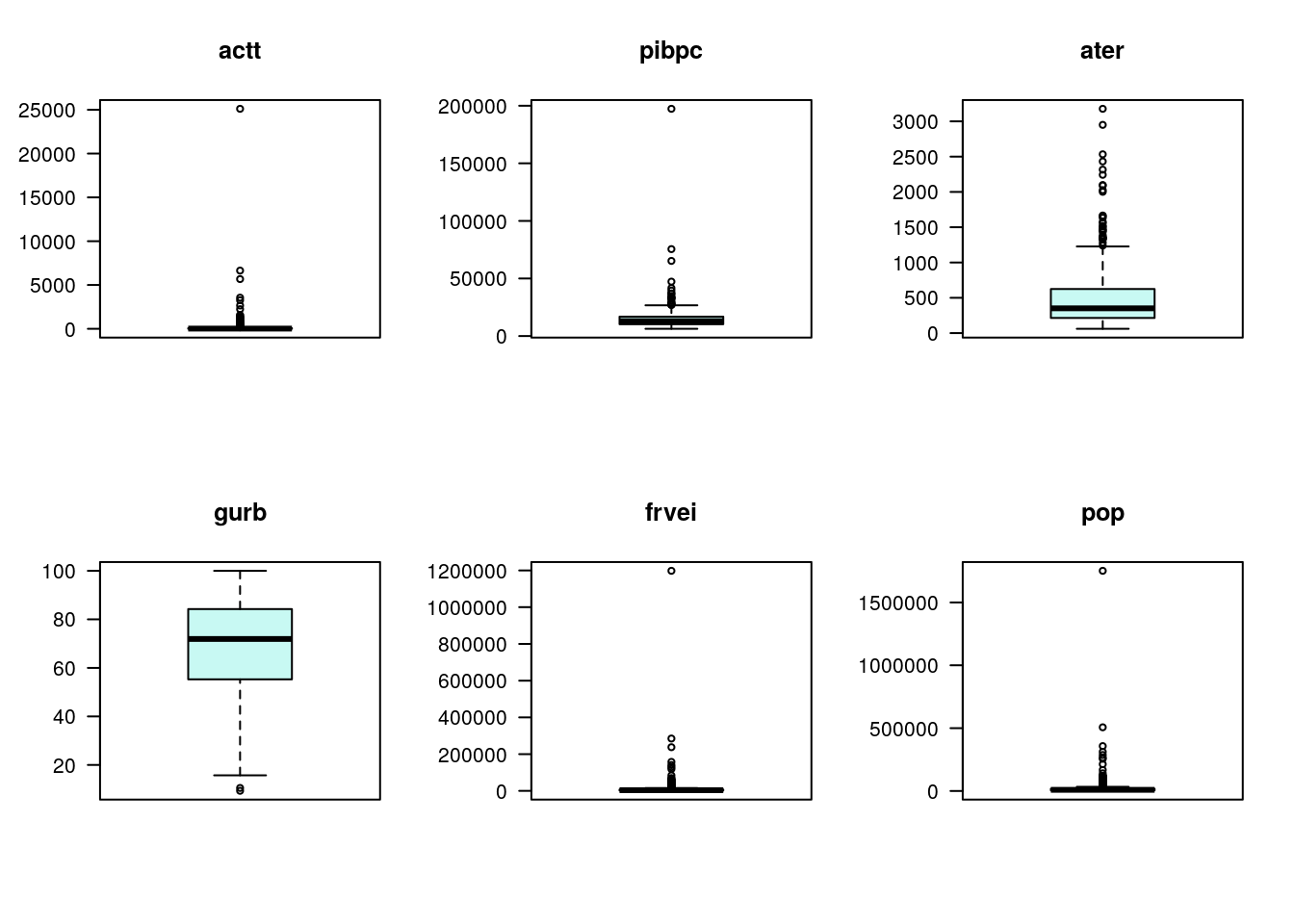
Nota-se nas variáveis número de acidentes, PIB, frota e população a presença de um ponto discrepante, muito mais alto que os demais. Em alguns casos pode ser conveniente trabalhar com o log da variável para obter uma maior simetria, outra alternativa é remover os valores discrepantes.

2.3 Histogramas

O histograma é outra alternativa para observar a forma da distribuição dos dados.

library(ggplot2)
library(gridExtra)

g1 <- ggplot(ipardes, aes(x=actt)) + geom_histogram()+ xlab('Acidentes de Trânsito')+ ylab('')
g2 <- ggplot(ipardes, aes(x=pibpc)) + geom_histogram()+ xlab('PIB per capita')+ ylab('')
g3 <- ggplot(ipardes, aes(x=ater)) + geom_histogram()+ xlab('Área Territorial')+ ylab('')
g4 <- ggplot(ipardes, aes(x=gurb)) + geom_histogram()+ xlab('Grau de Urbanização')+ ylab('')
g5 <- ggplot(ipardes, aes(x=frvei)) + geom_histogram()+ xlab('Frota de Veículos')+ ylab('')
g6 <- ggplot(ipardes, aes(x=pop)) + geom_histogram()+ xlab('População')+ ylab('')

grid.arrange(g1, g2, g3, g4, g5, g6, nrow=2, ncol=3)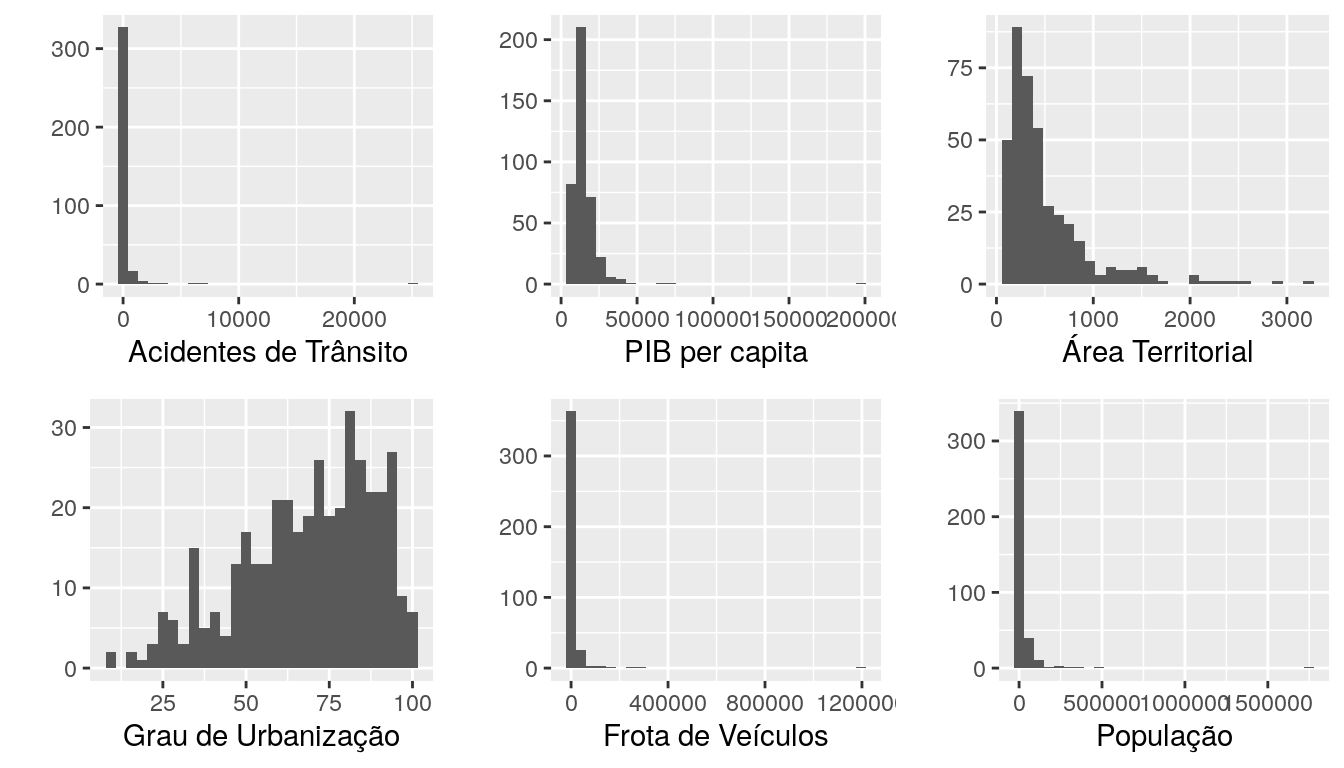

Os histogramas mostram uma considerável assimetria nas variáveis pib per capita, área territorial, frota e população, nestas variáveis pode ser considerada uma transformação.

O gráfico que corresponde ao histograma do número de acidentes de trânsito por munícipio é consideravelmente assimétrico devido à presença de municípios com número de acidentes muito maior que os demais, algumas delas são:

ipardes[c(70, 95, 121, 193, 211, 277, 352), ]

##                         cidade  actt pibpc     ater   gurb   frvei     pop
## 70                    Cascavel  3555 18578 2091.401  94.36  157748  286205
## 95                    Curitiba 25109 33177  435.495 100.00 1197974 1751907
## 121           Foz do Igua\xe7u  2660 24388  610.209  99.17  118804  256088
## 193                   Londrina  5676 21360 1656.606  97.40  284867  506701
## 211                 Maring\xe1  6644 23958  486.433  98.20  237656  357077
## 277               Ponta Grossa  3259 21497 2025.697  97.79  140331  311611
## 352 S\xe3o Jos\xe9 dos Pinhais  2241 65244  944.280  89.66  129319  264210

2.4 Transformação das variáveis explicativas

Vamos aplicar uma transformação logaritmica nas variáveis apontadas como mais assimétricas na análise descritiva:

ipardes$lpibpc <- log(ipardes$pibpc)
ipardes$later  <- log(ipardes$ater)
ipardes$lfrvei <- log(ipardes$frvei)
ipardes$lpop   <- log(ipardes$pop)

E verificar novamente a forma da distribuição das variáveis transformadas:

par(mfrow = c(1,4))

hist(ipardes$later, main = 'log(Área)', xlab = '', ylab = '', col = '#F3EBAB')
hist(ipardes$lfrvei, main = 'log(Frota)', xlab = '', ylab = '', col = '#F3EBAB')
hist(ipardes$lpibpc, main = 'log(PIB)', xlab = '', ylab = '', col = '#F3EBAB')
hist(ipardes$lpop, main = 'log(População)', xlab = '', ylab = '', col = '#F3EBAB')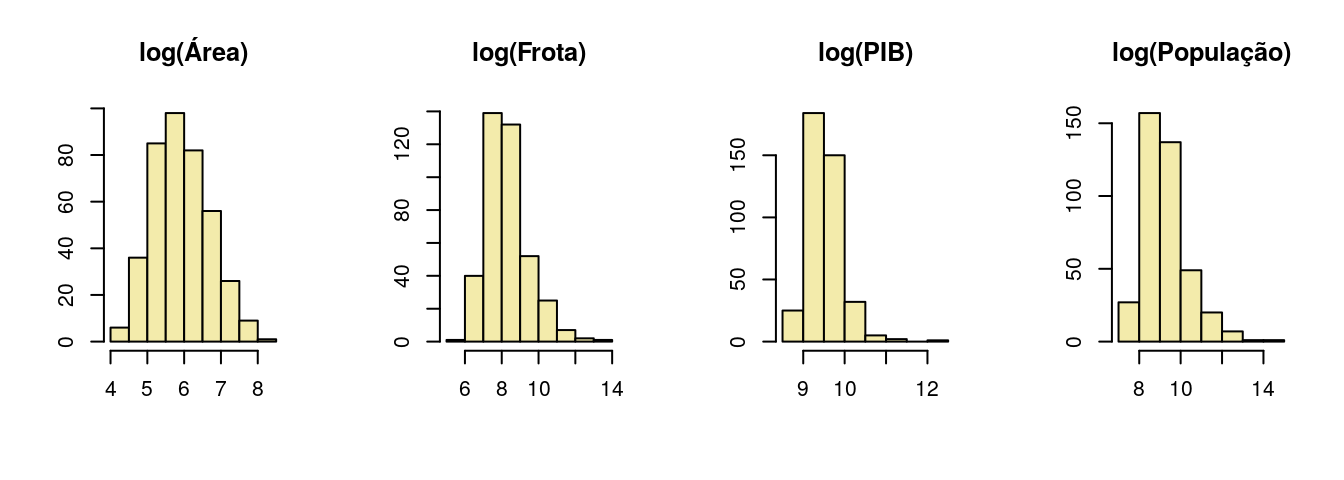

E agora sim verifica-se uma simetria bem maior na distribuição das covariáveis utilizadas.

2.5 Correlação

Nesta etapa vamos considerar as variáveis pib per capita, área territorial, frota e população transformadas.

A variável resposta do estudo possui dados faltantes, para resolver este problema é possível obter a correlação desta com as demais utilizando o argumento use da função cor

cor <- cor(ipardes[ , c(2,5,8,9,10,11)], use = "na.or.complete")

library(corrplot)
corrplot.mixed(cor, upper = "ellipse")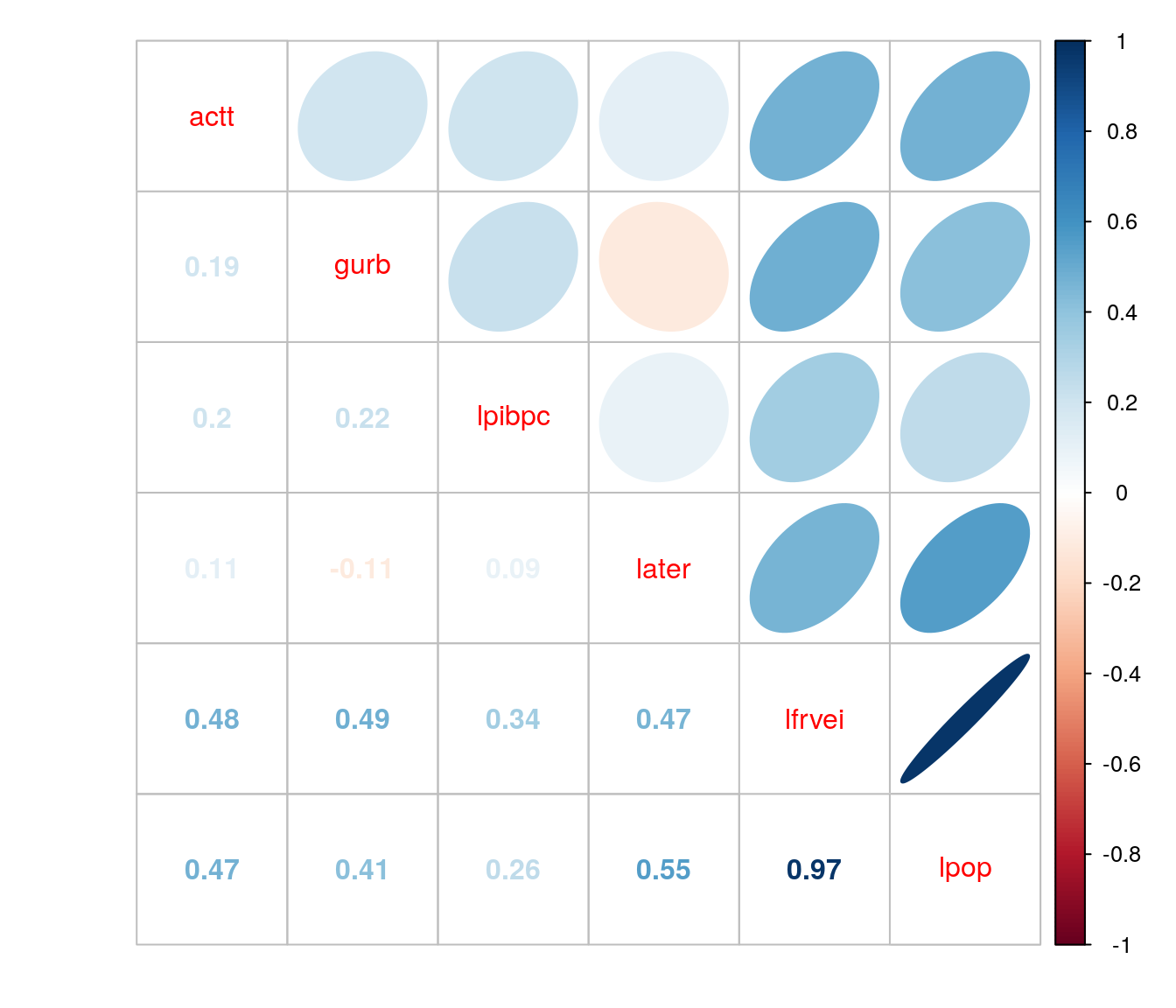

O correlograma aponta duas variáveis como mais correlacionadas com a resposta: o log da frota de veículos e o log da população. Nota-se também que essas duas variáveis são altamente correlacionadas entre si. Para fins de análise, ambas são possíveis candidatas à offssets.

2.6 Gráficos de Dispersão

plot(ipardes[ , c(2,5,8,9,10,11)] , 
     pch=20 , 
     cex=1.5 , 
     col=rgb(0.5, 0.8, 0.9, 0.7))

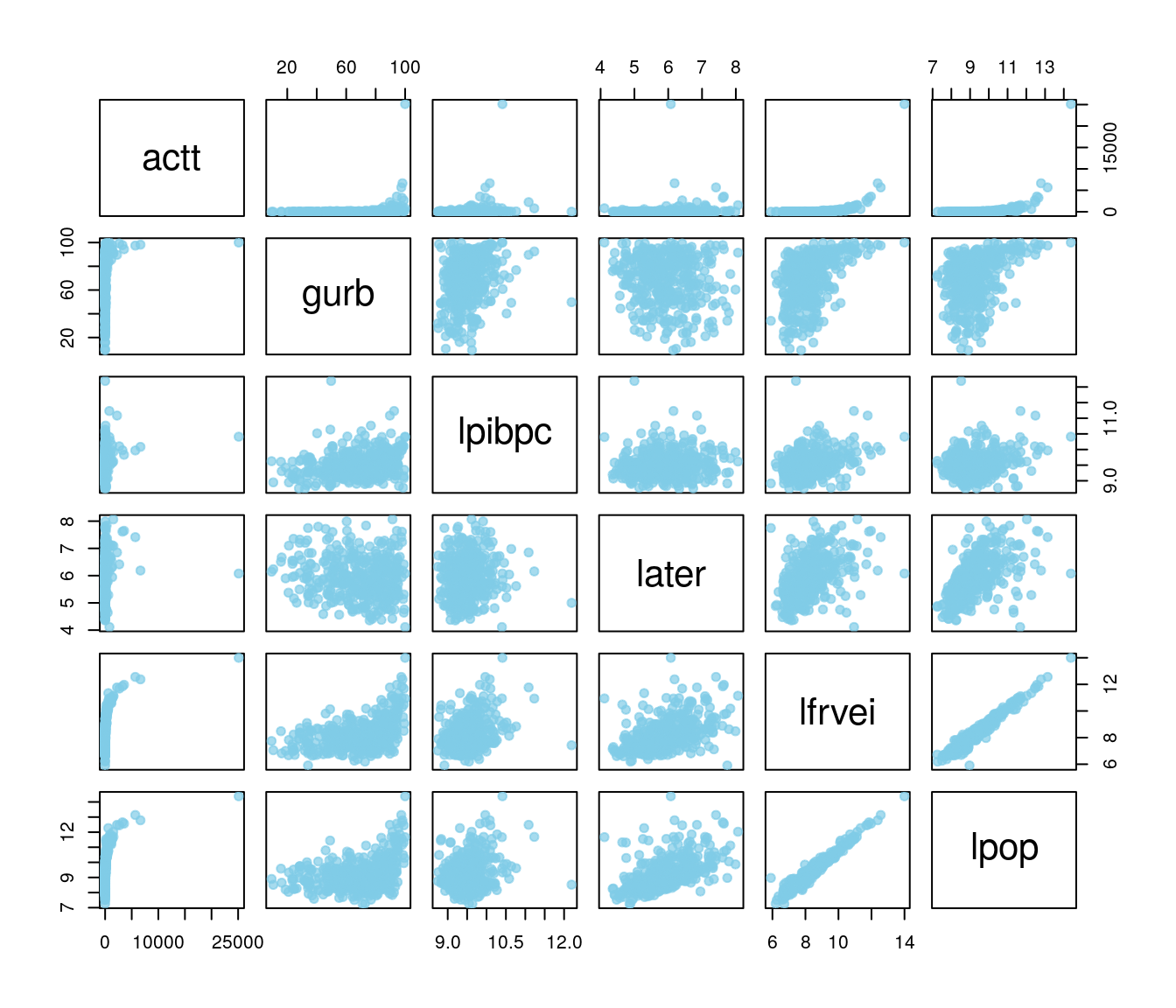
A matriz de gráficos de dispersão evidencia a alta relação entre as variáveis log da frota de veículos e o log da população; quanto à variável resposta nota-se a presença de valores altos atípicos, distantes da nuvem de pontos.

3 Ajuste dos Modelos de Regressão

A variável considerada como resposta é o número de ocorrências de um evento, neste caso é o número de acidentes de trânsito; trata-se portanto de uma variável de contagem, ou seja, uma variável discreta com suporte no conjunto dos inteiros não negativos. Para problemas como este deve-se buscar uma distribuição que comporte tais características; comumente a primeira alternativa de modelagem via modelo linear generalizado faz uso da distribuição de Poisson com função de ligação logaritmica.

Os modelos de regressão para dados de contagem com distribuição de probabilidades Poisson para a resposta são escritos da seguinte forma:

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}} \] \[y_{i}|\undertilde{x_{i}} \sim Poisson (\mu_{i})\]

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}}\]

\[ g(\mu_{i}) = {\beta_{0}} + {\beta_{1}}\, x_{i1} + {\beta_{2}}\, x_{i2} + ... + {\beta_{p}}\, x_{ip}\]

Em que \(y_{i}\) é a variável resposta, \(x_{i1}, x_{i2}, ..., x_{ip}\) correspondem às variáveis explicativas.

Além disso, \(g(\mu_{i})\) é a função de ligação. Se trata de uma função real, monótona e diferenciável, que associa e lineariza a relação entre o componente aleatório e o sistemático do modelo. A função de ligação canônica para um GLM Poisson é a logaritmica. Vale lembrar que como se trata de uma contagem, os valores preditos na escala da resposta não podem ser negativos e cabe à função de ligação garantir a não negatividade dos valores preditos.

Caso o GLM Poisson não se ajuste bem há outras opções de distribuições para a resposta. Uma das alternativas mais utilizadas é a Binomial Negativa. O principal diferencial dessa distribuição em relação à Poisson é que a Binomial Negativa comporta casos em que há superdispersão, enquanto na Poisson o parâmetro de dispersão deve ser fixo e igual a 1 (equidispersão, média igual à variância).

Nas subseções seguintes são mostrados os ajustes dos Modelos Lineares Generalizados log-linear de Poisson e com distribuição Binomial Negativa para a resposta.

3.1 GLM com resposta Poisson

Vamos ajustar um Modelo Linear Generalizado Poisson com função de ligação logaritmica e com as covariáveis inclusas de forma aditiva no modelo. A expressão do modelo é dada por:

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}} \]

\[y_{i}|\undertilde{x_{i}} \sim Poisson (\mu_{i})\]

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}}\]

\[ log(\mu _{i}) = {\beta_{0}} + {\beta_{1}}\, lpibpc_{i} + {\beta_{2}}\, later_{i} + {\beta_{3}}\, gurb_{i} +\ {\beta_{4}}\, lfrvei_{i} + {\beta_{5}}\, lpop_{i}\]

No R, o modelo é declarado da seguinte forma:

m1 <- glm(actt ~ lpibpc + later + gurb + lfrvei + lpop, data = ipardes, family = 'poisson')

3.2 GLM com resposta Binomial Negativa

Vamos ajustar um Modelo Linear Generalizado com distribuição Binomial negativa com função de ligação logaritimica. A expressão do modelo é igual ao do modelo Poisson, porém a distribuição da resposta tem forma diferente.

No R, o modelo é declarado da seguinte forma:

library(MASS)

m2 <- glm.nb(actt ~ lpibpc + later + gurb + lfrvei + lpop, data = ipardes)

4 Escolha do Modelo

Para seleção de modelos diversas medidas podem ser utilizadas, em especial vamos utilizar a verossimilhança e o AIC dos modelos. vale lembrar que o modelo Binomial Negativo estima um parâmetro de dispersão que não existe no modelo Poisson.

ajuste = c('m1', 'm2')

aic    = c(AIC(m1), AIC(m2))

verossimilhança = c(logLik(m1),logLik(m2))

data.frame(ajuste, aic, verossimilhança)

##   ajuste      aic verossimilhança
## 1     m1 8533.970       -4260.985
## 2     m2 2980.105       -1483.052

O modelo que apresentou menor AIC e maior verossimilhança foi o modelo Binomial Negativo. Adicionalmente, vamos verificar o comportamento dos gráficos meio Normais de probabilidades com envelopes simulados.

Esses gráficos permitem verificar a adequação do modelo ajustado mesmo que os resíduos não tenham uma aproximação adequada com a distribuição Normal. Sendo assim, neste tipo de gráfico espera-se, para um modelo bem ajustado, os pontos (resíduos) dispersos aleatoriamente entre os limites do envelope.

Deve-se ficar atento à presença de pontos fora dos limites do envelope ou ainda a pontos dentro dos limites porém apresentando padrões sistemáticos.

library(hnp)

par(mfrow = c(1,2))

hnp(m1, xlab = 'Percentil da N(0,1)', 
    ylab = 'Resíduos', 
    main = 'Poisson')

hnp(m2, xlab = 'Percentil da N(0,1)', 
    ylab = 'Resíduos', 
    main = 'Binomial Negativa')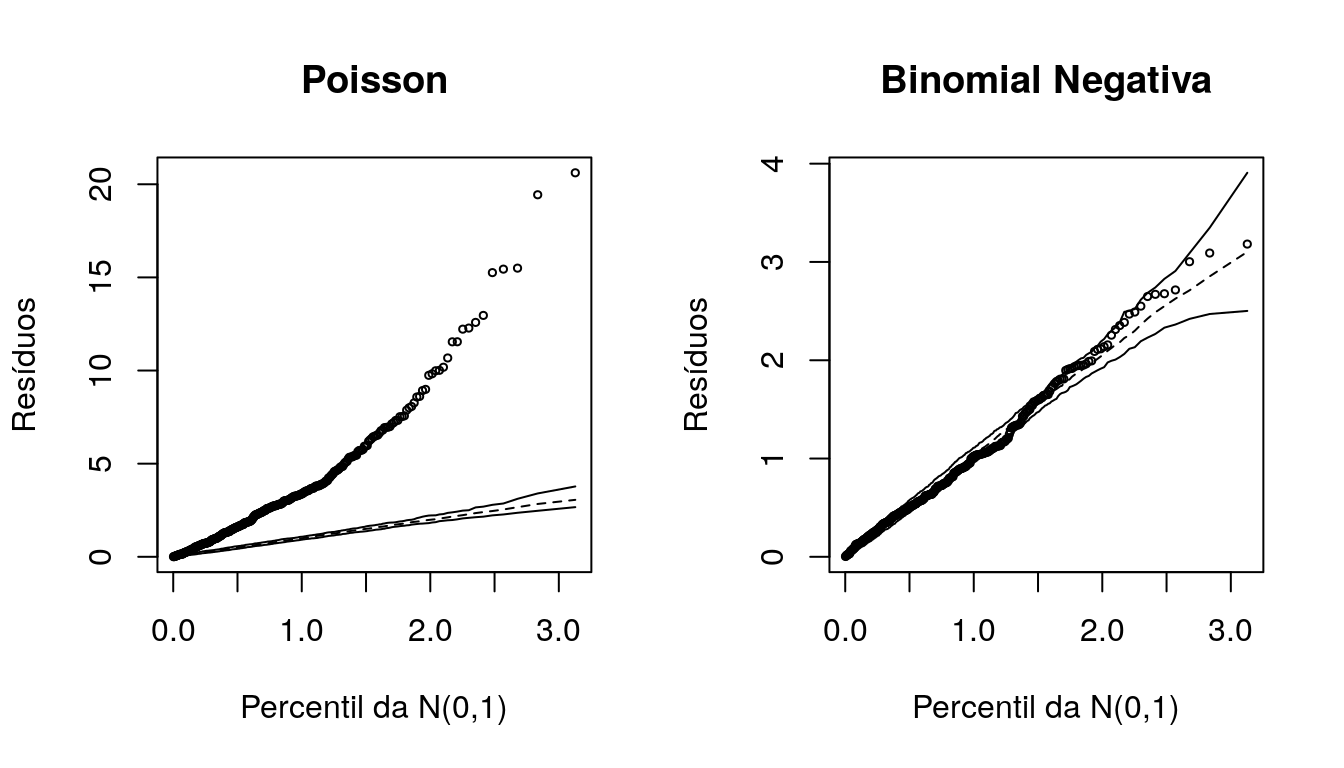

Nota-se pelas medidas de qualidade de ajuste e o comportamento dos resíduos no gráfico a total falta de aderência à distribuição de Poison; alterando a distribuição da resposta para Binomial Negativa obteve-se um ajuste satisfatório.

5 Modelo Escolhido

Vamos seguir as análises fazendo uso do modelo Binomial Negativo.

5.1 Resumo do Modelo

O modelo original foi ajustado usando todas as covariáveis disponíveis. Vamos verificar no resumo do modelo selecionado quais covariáveis são apontadas como significativas:

summary(m2)

## 
## Call:
## glm.nb(formula = actt ~ lpibpc + later + gurb + lfrvei + lpop, 
##     data = ipardes, init.theta = 3.664147641, link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.1819  -0.8559  -0.1779   0.4794   3.0907  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -10.216771   0.891832 -11.456  < 2e-16 ***
## lpibpc        0.134996   0.083845   1.610    0.107    
## later         0.055948   0.055061   1.016    0.310    
## gurb          0.011501   0.002046   5.620 1.91e-08 ***
## lfrvei        1.171845   0.156376   7.494 6.69e-14 ***
## lpop          0.141566   0.168776   0.839    0.402    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(3.6641) family taken to be 1)
## 
##     Null deviance: 5472.55  on 354  degrees of freedom
## Residual deviance:  382.48  on 349  degrees of freedom
##   (44 observations deleted due to missingness)
## AIC: 2980.1
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  3.664 
##           Std. Err.:  0.342 
## 
##  2 x log-likelihood:  -2966.105

O resumo do modelo ajustado indica que as variáveis grau de urbanização e log da frota de veículos foram significativas. No resumo é mostrado também o valor do parâmetro de dispersão (neste caso vale 3,6), muito maior que 1, o que explica a falta de ajuste à distribuição de Poisson.

5.2 Reajuste do Modelo

Como há um par de covariáveis altamente correlacionadas (log da frota e log da população), é válido inserir as covariáveis uma a uma no modelo para verificar sua significância na presença das outras; tal como o realizado pelo algoritmo stepwise. Notou-se que ao retirar a variável log da frota, o log da população se mostra significativo.

Sendo assim, o novo modelo fica da seguinte forma:

m2.1 <- step(m2, direction = "both")

O resumo do novo modelo ajustado:

summary(m2.1)

## 
## Call:
## glm.nb(formula = actt ~ gurb + lfrvei, data = ipardes, init.theta = 3.615959105, 
##     link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.0461  -0.8343  -0.1949   0.4698   3.2940  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -8.603487   0.231379 -37.183  < 2e-16 ***
## gurb         0.010333   0.001837   5.625 1.85e-08 ***
## lfrvei       1.340227   0.030368  44.133  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(3.616) family taken to be 1)
## 
##     Null deviance: 5405.25  on 354  degrees of freedom
## Residual deviance:  383.23  on 352  degrees of freedom
##   (44 observations deleted due to missingness)
## AIC: 2978.6
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  3.616 
##           Std. Err.:  0.336 
## 
##  2 x log-likelihood:  -2970.646

O algoritmo indica que as variáveis grau de urbanização e log da frota são significativas e tem relação positiva com o número de acidentes de trânsito.

Agora, vamos realizar o teste da razão de verossimilhança do modelo inicial e do reduzido:

anova(m2, m2.1)

## Likelihood ratio tests of Negative Binomial Models
## 
## Response: actt
##                                   Model    theta Resid. df    2 x log-lik.
## 1                         gurb + lfrvei 3.615959       352       -2970.646
## 2 lpibpc + later + gurb + lfrvei + lpop 3.664148       349       -2966.105
##     Test    df LR stat.   Pr(Chi)
## 1                                
## 2 1 vs 2     3 4.540832 0.2086769

O p-valor do teste foi relativamente alto, portanto pode-se concluir que o modelo restrito se ajusta aos dados amostrais tão bem quanto o modelo considerando todas as covariáveis. Portanto o modelo final fica expresso por:

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}} \]

\[y_{i}|\undertilde{x_{i}} \sim Binomial\; Negativa (\mu_{i}, \phi)\]

\[ \newcommand{\undertilde}[1]{\underset{\widetilde{}}{#1}}\]

\[ \log(\mu _{i}) = { -8.60349} + {0.01033}\, gurb_{i} + {1.34023}\, log(frvei_{i})\]

5.3 Medidas de Influência

Uma alternativa para verificação de medidas influentes está implementada no pacote car:

library(car)

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some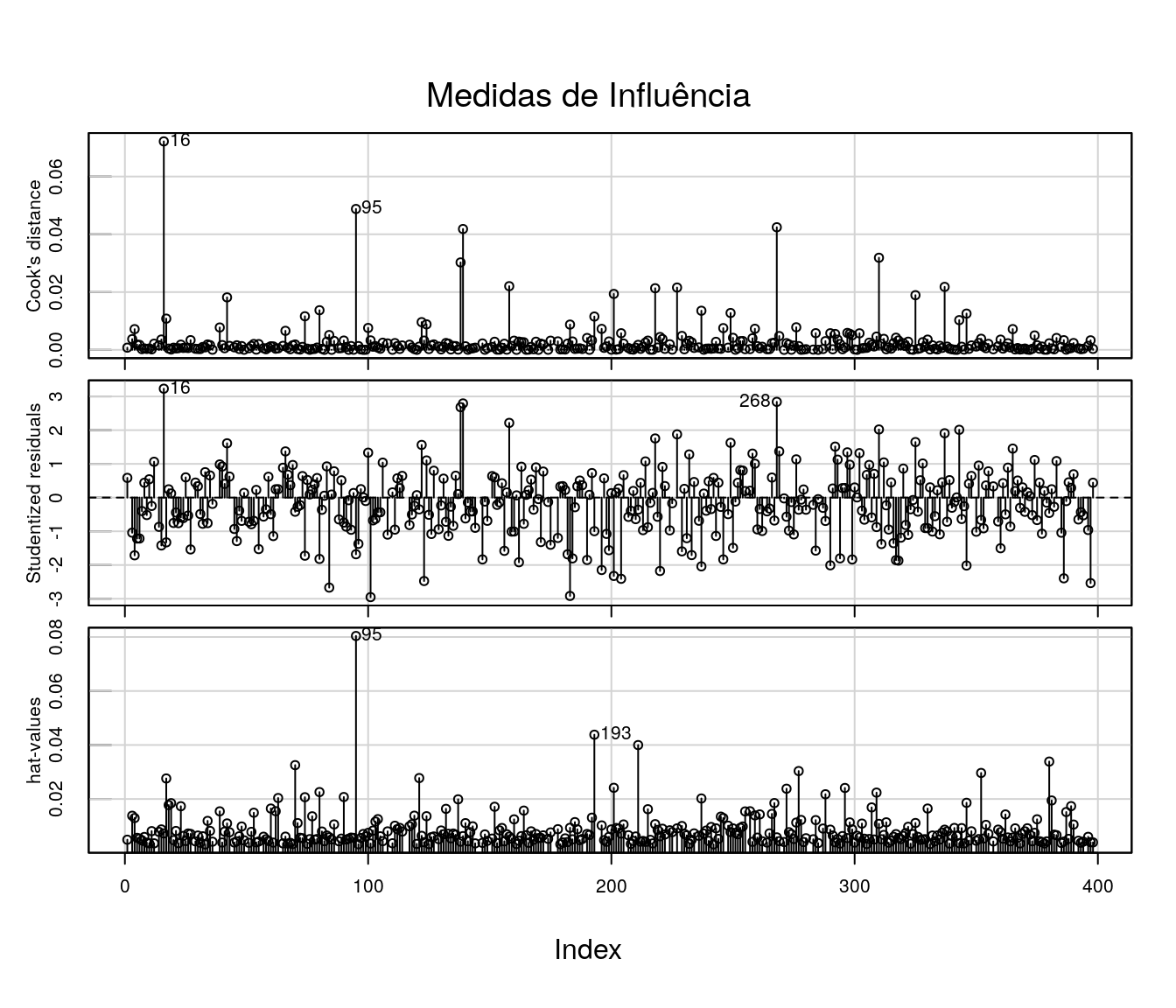

influenceIndexPlot(m2.1, vars=c("Cook", "Studentized", "hat"), main="Medidas de Influência")

O primeiro gráfico apresenta os valores da distância de Cook para cada observação. A distância de Cook é uma medida de diferença das estimativas dos parâmetros do modelo ao considerar e ao desconsiderar uma particular observação no ajuste.

O segundo gráfico mostra os resíduos studentizados; um modelo bem ajustado apresenta estes resíduos dispersos aleatóriamente em torno de 0, entre -3 e 3 desvios.

O terceiro gráfico mostra os valores da matriz chapéu (H). Valores elevados são considerados potencialmente influentes. Os valores da matriz chapéu estão entre 0 e 1. A soma dos elementos da diagonal da matriz H equivale ao posto da matriz X de delineamento.

Com base nesses 3 gráficos, não há indicativos fortes de outliers ou observações influentes.

5.4 Resíduos Quantílicos Aleatorizados

Outra alternativa para avaliar a qualidade do ajuste é baseada nos resíduos quantílicos aleatorizados. A função qresiduals do pacote statmod extrai este tipo de resíduos do modelo

library(statmod)

par(mfrow=c(1,2))

res <- qresiduals(m2.1)

plot(res)

residuos <- qresiduals(m2.1)
qqnorm(residuos)
qqline(residuos, col = 2)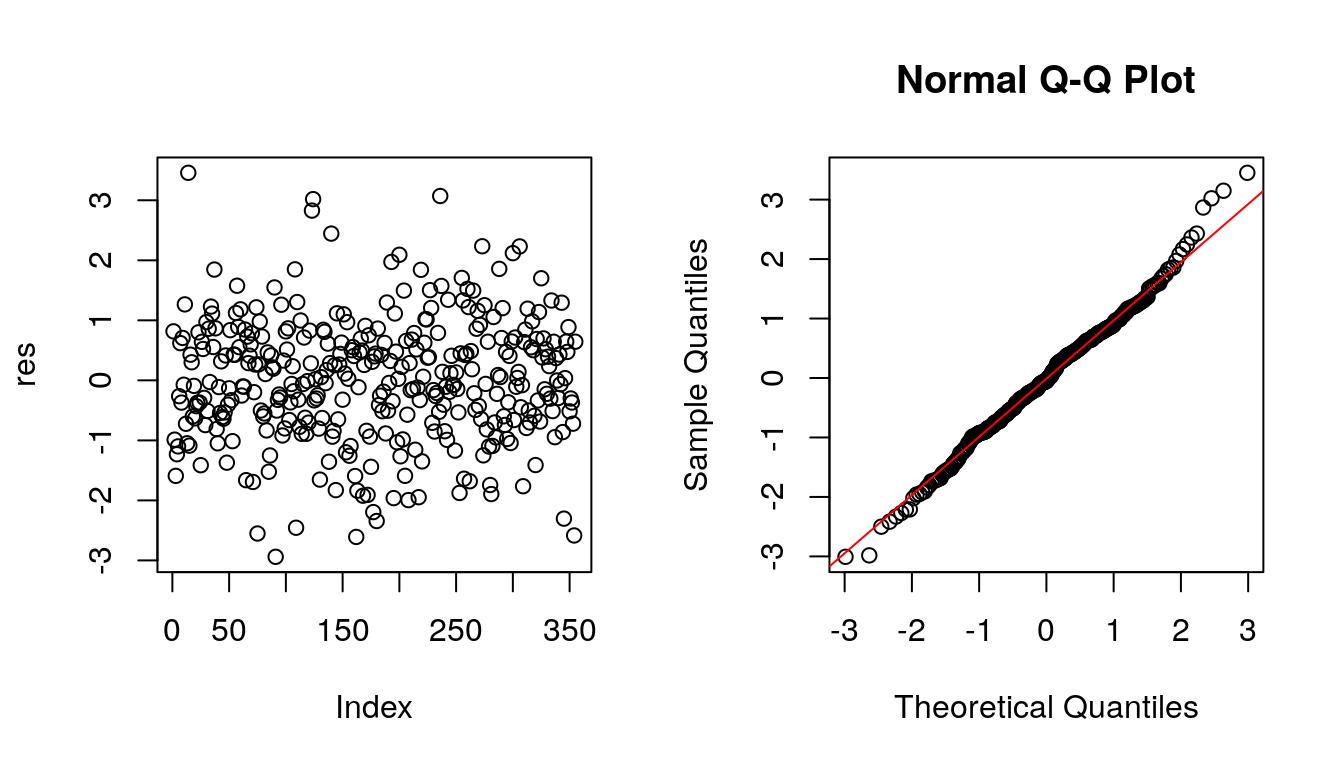

No gráfico da esquerda nota-se que os resíduos estão dispersos predominantemente em torno de 0 entre -2 e 2. Além disso, no gráfico a direita verifica-se que os resíduos apresentam razoável aderência à distribuição Normal. Há um leve indício de caudas pesadas; porém, no geral, parece que há um ajuste plausível.

5.5 Gráfico Normal de Probabilidades com Envelope Simulado

Vamos verificar o comportamento do gráfico Normal de probabilidades com envelope simulado para o modelo reajustado:

hnp(m2, xlab = 'Percentil da N(0,1)', 
    ylab = 'Resíduos', 
    main = 'Gráfico Normal de Probabilidades')

## Negative binomial model (using MASS package)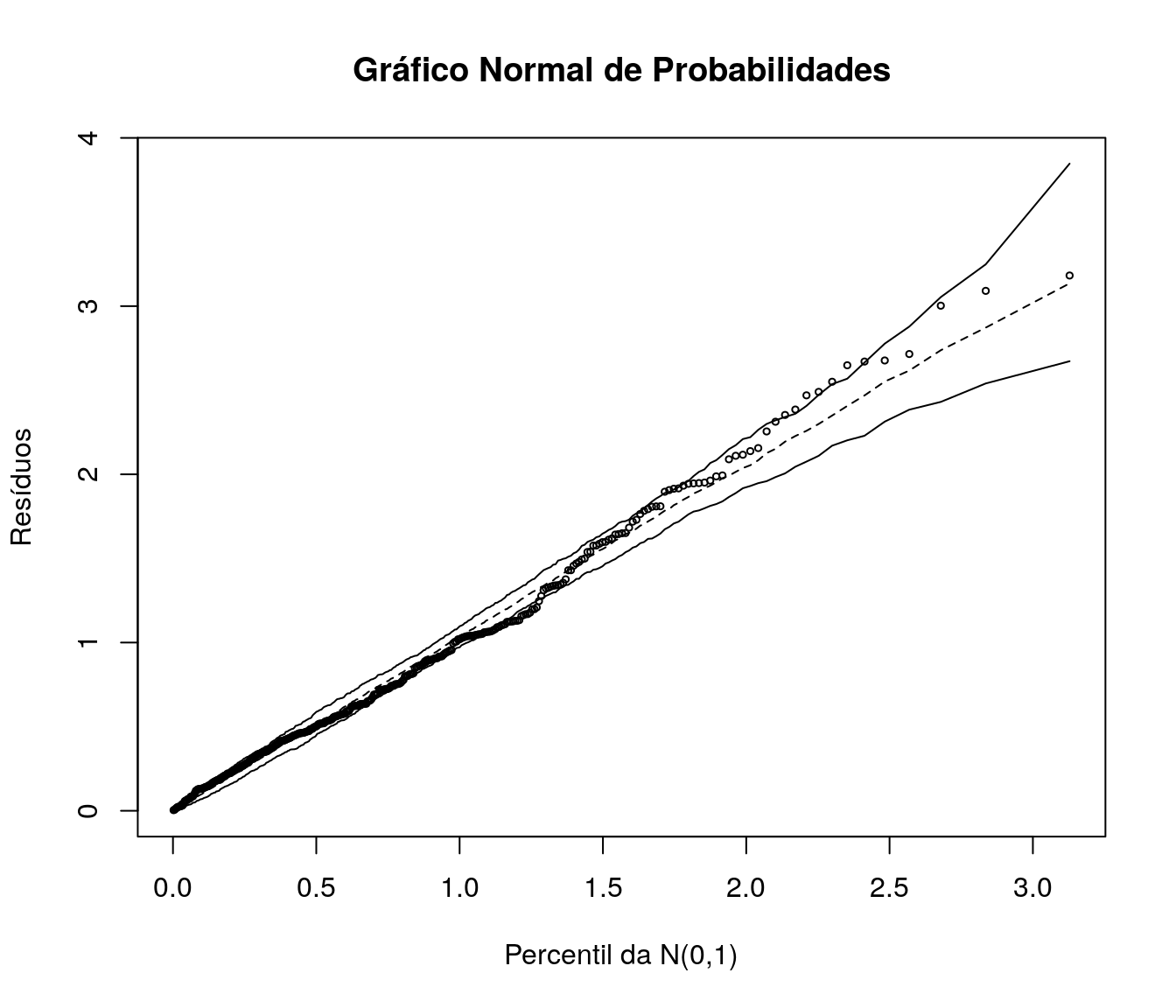

Os resíduos estão dispersos no interior dos envelopes simulados, sem aparente padrão sistemático dando indício de que o modelo está bem ajustado.

5.6 Gráficos de Efeitos

A função effects, do pacote de mesmo nome, devolve os efeitos marginais de cada variável de um modelo ajustado; os gráficos de efeitos nos fornecem uma forma visual de observar como cada variável explicativa afeta a resposta, com as demais variáveis fixadas na média.

library(effects)

## Registered S3 methods overwritten by 'lme4':
##   method                          from
##   cooks.distance.influence.merMod car 
##   influence.merMod                car 
##   dfbeta.influence.merMod         car 
##   dfbetas.influence.merMod        car

## lattice theme set by effectsTheme()
## See ?effectsTheme for details.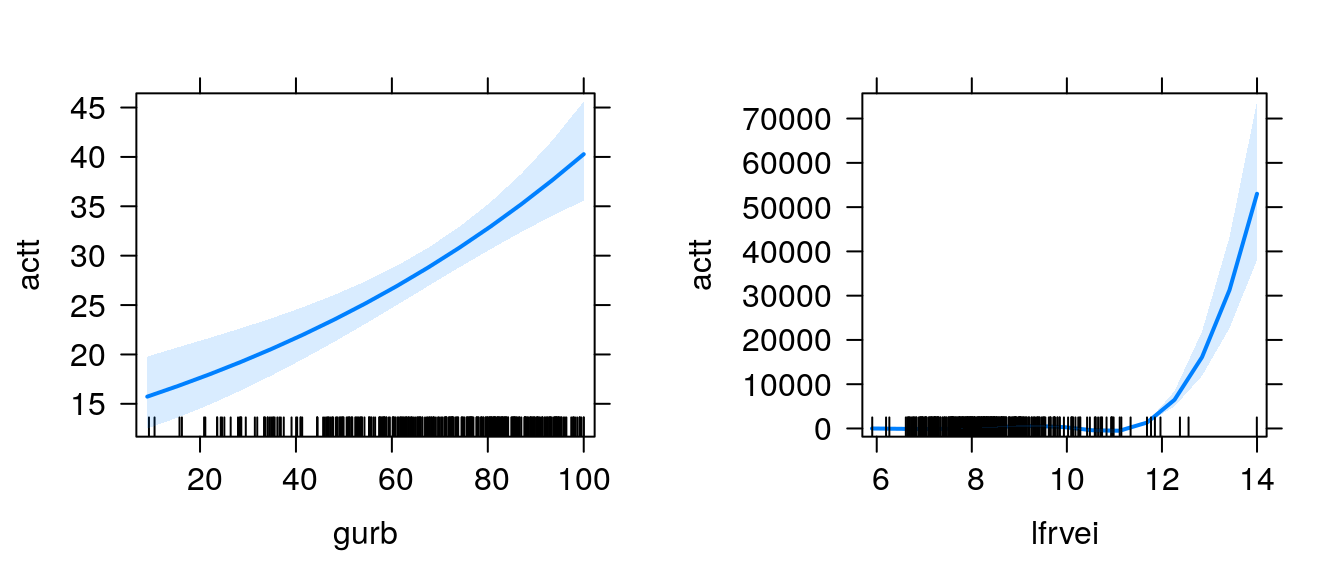

plot(allEffects(m2.1), type = 'response', main = '')

6 Predição

Para fins de ilustração, vamos considerar os seguintes perfis para três municípios distintos:

Perfil 1:

Grau de Urbanização = 10
Log da frota de veículos = 8

Perfil 2

Grau de Urbanização = 70
Log da frota de veículos = 10

Perfil 3

Grau de Urbanização = 100
Log da frota de veículos = 12

E responder à seguinte pergunta: Qual é o número esperado de acidentes de trânsito em municípios com o Perfil 1, 2 e 3?

perfis <- data.frame(gurb   =  c(10, 70, 100), 
                     lfrvei =  c(8,  10,  12))

Utilizando a função predict para obter o número esperado de acidentes nos perfis:

predict(m2.1, interval = 'prediction', newdata = perfis, type = 'response')

##           1           2           3 
##    9.222629  250.156084 4976.712891

Portanto, o número esperado de acidentes de trânsito para um município fictício com o Perfil 1 é igual a 9; para um município com o Perfil 2 este número passa para 250, e no teceiro perfil o número esperado de acidentes é de 4976.

7 Outra Abordagem: Quase-Verossimilhança

Os modelos de quase-verossimilhança são uma forma de modelagem mais flexível quando comparada aos modelos lineares generalizados; o método consiste em especificar um modelo baseado aoenas na média e variância da distribuição tornando-o mais flexível, o que muitas vezes é o suficiente para acomodar superdispersão nos dados.

Tais como os estimadores de máxima verossimilhança, os estimadores de máxima quase-verossimilhança são assintóticamente não viciados, consistentes e normalmente distribuídos.

7.1 Ajuste do modelo

Vamos reajustar o modelo por quase-verossimilhança:

mq <- glm(actt ~ lpibpc + later + gurb + lfrvei + lpop, data = ipardes, 
          family = quasi(variance = "mu^2", link = "log"))

7.2 Diagnóstico

Com o modelo ajustado pode-se realizar a análise de diagnóstico:

7.2.1 Medidas de Influência

Vamos iniciar com a verificação de possíveis medidas influentes:

library(car)

influenceIndexPlot(mq, vars=c("Cook", "Studentized", "hat"), main="Medidas de Influência")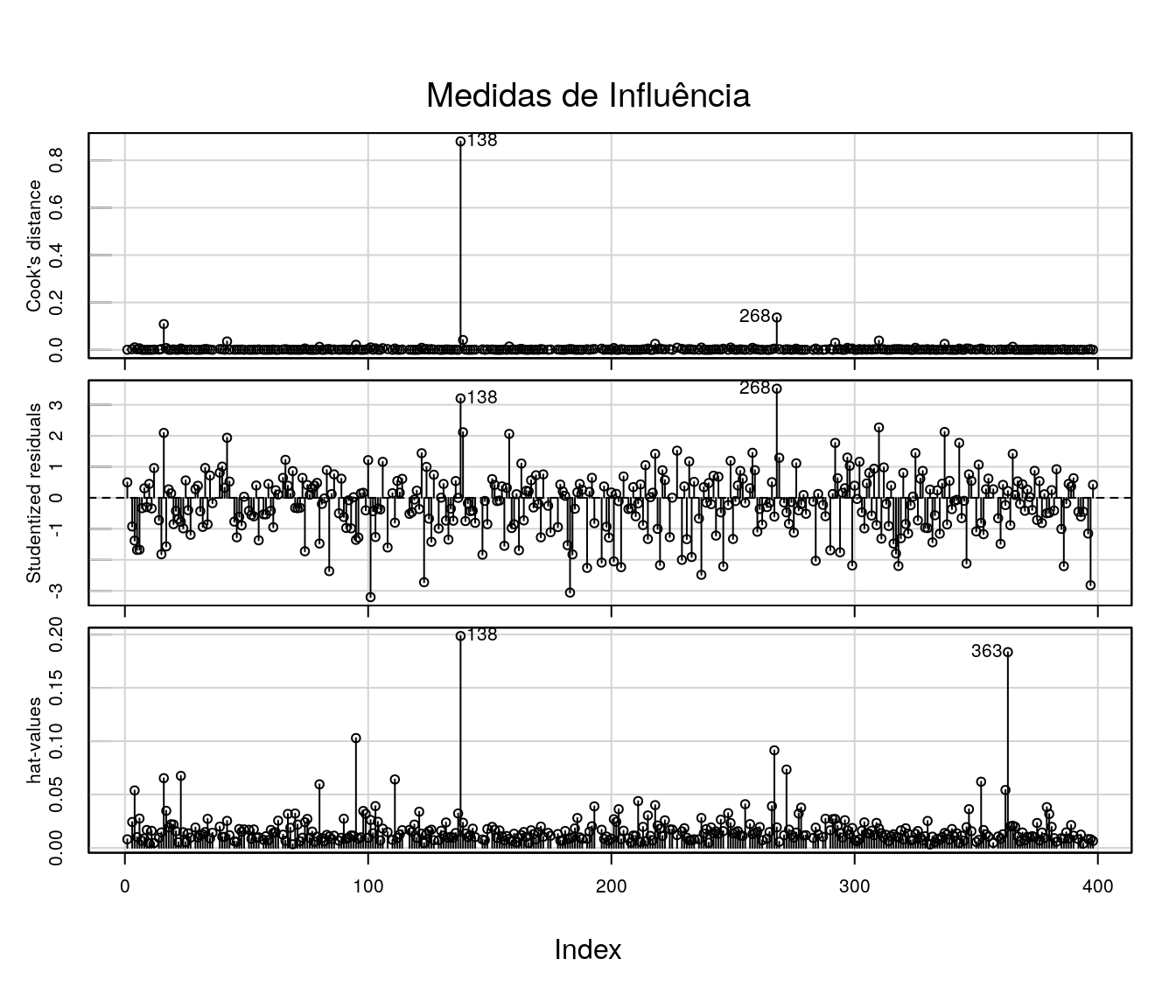

Uma das observações apontadas como fortemente influente é o município de Guaraqueçaba:

ipardes[138,]

##              cidade actt pibpc     ater  gurb frvei  pop   lpibpc    later
## 138 Guaraque\xe7aba    5  7438 2315.733 34.09   367 7871 8.914357 7.747482
##       lfrvei    lpop
## 138 5.905362 8.97094

7.2.2 Resíduos

qqnorm(resid(mq, type = "deviance"),
       pch = 20, main = "Resíduos do modelo de Quase-Verossimilhança", las = 1)

qqline(resid(mq, type = "deviance"), col = 2)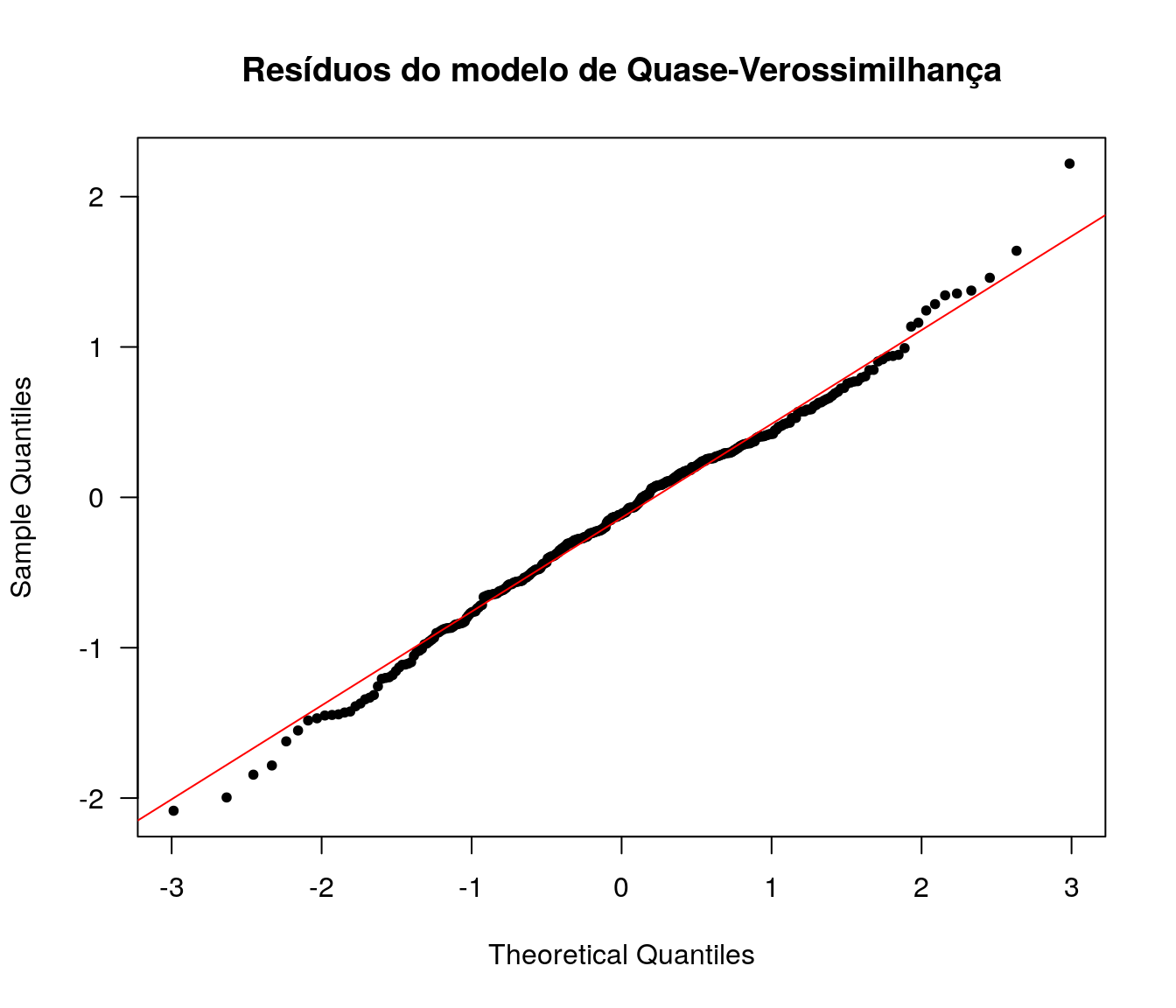

Os resíduos componentes da Deviance para o modelo de Quase-Verossimilhança ajustado têm distribuição aproximadamente Normal.

Sendo assim, o modelo de Quase-Verossimilhança é mais uma alternativa para modelagem de dados de contagem sendo que esta, diferente das duas primeiras apresentadas, tem enfoque não paramétrico.